题目内容
在△ABC中,a,b,c为∠A,∠B,∠C的对边,若cos2B+cosB+cos(A-C)=1,b=
,则a2+c2的最小值为 .
| 7 |
考点:余弦定理,正弦定理
专题:解三角形
分析:根据正弦定理,结合等差数列和等比数列的定义即可得到结论.
解答:
解:∵cos2B+cosB+cos(A-C)=1,
∴cos2B-cos(A+C)+cos(A-C)=1,
即1-2sin2B-cosAcosC+sinAsinC+cosAcosC+sinAsinC=1,
即sinAsinC=sin2B,
由正弦定理得ac=b2,(a,b,c>0),
∴a2+c2≥2ac=2b2=14.
故答案为:14.
∴cos2B-cos(A+C)+cos(A-C)=1,
即1-2sin2B-cosAcosC+sinAsinC+cosAcosC+sinAsinC=1,
即sinAsinC=sin2B,
由正弦定理得ac=b2,(a,b,c>0),
∴a2+c2≥2ac=2b2=14.
故答案为:14.
点评:本题主要考查等差数列的判断以及正弦定理的应用,要求熟练掌握相应的公式,属于基本知识的考查.

练习册系列答案
相关题目
已知函数f(x)=
,若f(x)≥ax恒成立,则a的取值范围是( )
|
A、(∞,
| ||||
B、[-
| ||||
C、[
| ||||
| D、[1,+∞) |
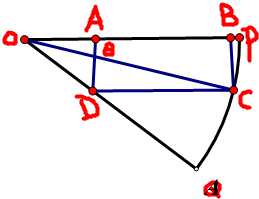 如图OPQ是半径为
如图OPQ是半径为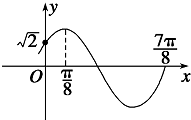 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<