题目内容
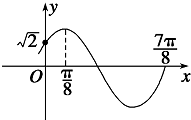 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
(1)求其解析式;
(2)令g(x)=
| f2(x)-2f(x)+2 |
| f(x)-1 |
| π |
| 4 |
考点:函数y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的求值,三角函数的图像与性质,不等式
分析:(1)首先根据函数的图象求出A、ω,φ的值,进一步确定函数的解析式.
(2)利用函数的变换求出g(x)的解析式,进一步利用单调性求出最值.
(2)利用函数的变换求出g(x)的解析式,进一步利用单调性求出最值.
解答:
解:(1)利用函数的图象:
=
-
=
所以:T=π
求得:ω=2
将点(
,0)代入sin(
+φ)=0
解得:φ=-
+2kπ(k∈Z)
由于:|φ|<
解得:φ=
将点(0,
)代入关系式:解得:A=2
所以:f(x)=2sin(2x+
)
(2)令g(x)=
=f(x)-1+
设m=f(x)-1=2sin(2x+
)-1
则:g(x)=m+
当0≤x≤
时,
≤2x+
≤
所以:
≤sin(2x+
)≤1
-1≤m≤1
由于g(x)=m+
在[
-1,1]上是减函数
则:当x=0或
时,g(x)取最大值.
g(x)max=2
| 3T |
| 4 |
| 7π |
| 8 |
| π |
| 8 |
| 3π |
| 4 |
所以:T=π
求得:ω=2
将点(
| 7π |
| 8 |
| 14π |
| 8 |
解得:φ=-
| 7π |
| 4 |
由于:|φ|<
| π |
| 2 |
解得:φ=
| π |
| 4 |
将点(0,
| 2 |
所以:f(x)=2sin(2x+
| π |
| 4 |
(2)令g(x)=
| f2(x)-2f(x)+2 |
| f(x)-1 |
| 1 |
| f(x)-1 |
设m=f(x)-1=2sin(2x+
| π |
| 4 |
则:g(x)=m+
| 1 |
| m |
当0≤x≤
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
所以:
| ||
| 2 |
| π |
| 4 |
| 2 |
由于g(x)=m+
| 1 |
| m |
| 2 |
则:当x=0或
| π |
| 4 |
g(x)max=2
| 2 |
点评:本题考查的知识要点:三角函数解析式的求法,及三角函数的最值问题,函数的单调性的应用.属于基础题型.

练习册系列答案
相关题目
已知等边△ABC中,点P在线段AB上,且
=λ
,若
•
=
•
,则实数λ的值为( )
| AP |
| PB |
| CP |
| AB |
| PA |
| PB |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
 某选手参加演讲比赛的一次评委打分如茎叶图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
某选手参加演讲比赛的一次评委打分如茎叶图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A、86.5,1.5 |
| B、86.5,1.2 |
| C、86,1.5 |
| D、86,1.2 |
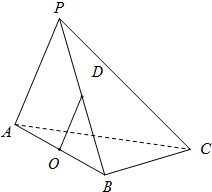 在三棱锥P-ABC中△PAC,△PBC是边长为
在三棱锥P-ABC中△PAC,△PBC是边长为 为了解我县中学生的体质状况,对天义地区部分中学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如下表所示.
为了解我县中学生的体质状况,对天义地区部分中学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如下表所示.