题目内容
已知函数f(x)=
,若f(x)≥ax恒成立,则a的取值范围是( )
|
A、(∞,
| ||||
B、[-
| ||||
C、[
| ||||
| D、[1,+∞) |
考点:分段函数的应用
专题:函数的性质及应用
分析:先把函数化为分段函数,画出函数的图象,令y=f(x)、y=ax,f(x)≥ax恒成立等价于函数y=f(x)的图象位于函数y=ax的上方.
解答:
解:当-2≤x≤0时,f(x)=1-(
x+1)=-
x;当x<-2时,f(x)=1+(
x+1)=
x+2;
函数化为f(x)=
,
其图象如下:

其中,直线n1与直线AB平行,故斜率为kn1=kAB=
=
,
直线n2是直线y=ax与曲线y=ex-1相切于原点的直线,故斜率kn2=y′|x=0=ex|x=0=e0=1,
要使f(x)≥ax恒成立,只有使直线y=ax在图中阴影区域,也即位于直线n1与n2 之间,
∴直线y=ax的斜率a应满足:kn1≤a≤kn2,
∴
≤a≤1
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
函数化为f(x)=
|
其图象如下:

其中,直线n1与直线AB平行,故斜率为kn1=kAB=
| 1-0 |
| -2+4 |
| 1 |
| 2 |
直线n2是直线y=ax与曲线y=ex-1相切于原点的直线,故斜率kn2=y′|x=0=ex|x=0=e0=1,
要使f(x)≥ax恒成立,只有使直线y=ax在图中阴影区域,也即位于直线n1与n2 之间,
∴直线y=ax的斜率a应满足:kn1≤a≤kn2,
∴
| 1 |
| 2 |
故选:C.
点评:本题考查分段函数的图象和运用,考查数形结合的思想方法,以及不等式恒成立的思想,属于中档题.

练习册系列答案
相关题目
下列函数中,在(0,+∞)既是增函数又是奇函数的是( )
| A、y=x+1 | ||
B、y=x+
| ||
C、y=x-
| ||
| D、y=x2+1 |
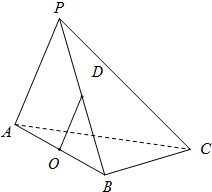 在三棱锥P-ABC中△PAC,△PBC是边长为
在三棱锥P-ABC中△PAC,△PBC是边长为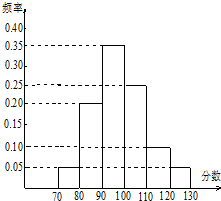 某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括
某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括