题目内容
已知点A,B分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,AB中点M(x0,y0),且y0≥x0+2,则x0-y0的最大值为 .
考点:两点间的距离公式
专题:直线与圆
分析:设出A,B的坐标,由中点坐标公式得到M的坐标与A,B的坐标的关系,y1+y2=t,得到关于t的不等式,求出t的范围后再把x0-y0转化为t的代数式得答案.
解答:
解:令A(x1,y1)、B(x2,y2),则x0=
,y0=
,
由y0≥x0+2,得
≥
+2,
令y1+y2=t,则t≥6-
+4,得t≥
.
x0-y0=3-
-
=3-
t,
∵t≥
,
∴3-
t≤-2.
故答案为:-2.
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
由y0≥x0+2,得
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
令y1+y2=t,则t≥6-
| t |
| 2 |
| 20 |
| 3 |
x0-y0=3-
| t |
| 4 |
| t |
| 2 |
| 3 |
| 4 |
∵t≥
| 20 |
| 3 |
∴3-
| 3 |
| 4 |
故答案为:-2.
点评:本题考查了两点间的距离公式,考查了数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若实数x,y满足线性约束条件
,则z=2x+y的最大值为( )
|
| A、0 | B、4 | C、5 | D、7 |
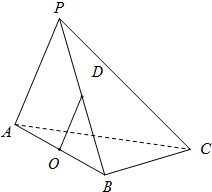 在三棱锥P-ABC中△PAC,△PBC是边长为
在三棱锥P-ABC中△PAC,△PBC是边长为