Question

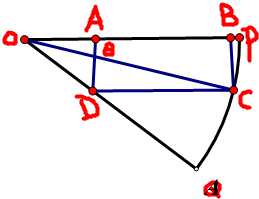如图OPQ是半径为

2

，圆心角为

π

4

的扇形，ABCD是扇形OPQ的内接距形，A，B在OP上，点D在OQ上，点C在弧PQ上，记∠POQ=θ；
（Ⅰ）用含θ的式子表示AB的长；
（Ⅱ）记距形ABCD的面积为f（θ），求f（θ）的单调区间和最大值．

Answer 1

考点：已知三角函数模型的应用问题

专题：综合题,三角函数的求值

分析：（Ⅰ）求出OB，OA，即可用含θ的式子表示AB的长；
（Ⅱ）由（Ⅰ）得f（θ）=|AB||BC|=（

2

cosθ-

2

sinθ）

2

sinθ，先化简，再求f（θ）的单调区间和最大值．

解答： 解：（Ⅰ）由∠POC=θ，ABCD为矩形，OC=

2

得AD=BC=

2

sinθ，OB=

2

cosθ
又∠POQ=45°，∴OA=AD=

2

sinθ，
∴|AB|=

2

cosθ-

2

sinθ；
（Ⅱ）由（Ⅰ）得f（θ）=|AB||BC|=（

2

cosθ-

2

sinθ）

2

sinθ，
=sin2θ-1+cos2θ=

2

sin（2θ+

π

4

）-1，θ∈（0，

π

4

），
∵θ∈（0，

π

4

），
∴2θ+

π

4

∈（

π

4

，

3π

4

），
∴θ∈（0，

π

8

）时，y=f（θ）为增函数；θ∈（

π

8

，

π

4

）时，y=f（θ）为减函数；
∴y=f（θ）的增区间为（0，

π

8

），减区间为（

π

8

，

π

4

），
∴f（θ）_max=f（

π

8

）=

2

-1．

点评：本题考查三角函数模型的应用问题，考查学生分析解决问题的能力，确定三角函数的模型是关键．