题目内容
15.Sn是数列{an}的前n项和,且a1=1,an+1=2an+n-1,S10=1991.分析 由数列{an}满足a1=1,an+1=2an+n-1,变形为an+1+(n+1)=2(an+n),即可数列{an+n}是等比数列,其中首项为a1+1=2,公比为2.求出通项公式
再利用等比数列的通项公式、等比数列与等差数列的前n项和公式即可得出,代值计算即可.
解答 解:由数列{an}满足a1=1,an+1=2an+n-1,变形为an+1+(n+1)=2(an+n).
∴数列{an+n}是等比数列,其中首项为a1+1=2,公比为2,
∴an+n=2×2n-1,
∴an=2n-n
∴Sn=$\frac{2({2}^{n}-1)}{2-1}$-$\frac{n(n+1)}{2}$=2n+1-2-$\frac{n(n+1)}{2}$,
∴S10=211-2-$\frac{10(10+1)}{2}$=1991
故答案为:1991.
点评 本题考查了数列的递推公式和等比数列的通项公式、等比数列与等差数列的前n项和公式,属于中档题.

练习册系列答案
相关题目
5.若直线x-y-m=0被圆x2+y2-8x+12=0所截得的弦长为$2\sqrt{2}$,则实数m的值为( )
| A. | 2或6 | B. | 0或8 | C. | 2或0 | D. | 6或8 |
12.若方程E:$\frac{x^2}{1-m}-\frac{y^2}{m-2}$=1表示焦点在y轴上的双曲线,则实数m的取值范围为( )
| A. | (1,2) | B. | (-∞,1)∪(2,+∞) | C. | (-∞,2) | D. | (1,+∞) |
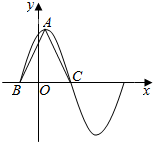 函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.