题目内容
19.执行如图的程序框图,则输出的S=( )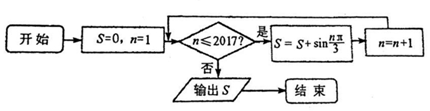
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | 0 |
分析 模拟程序的运行,依次写出前几次循环得到的S,n的值,观察规律可知,S的取值以6为最小正周期循环,由于2017=336×6+1,可得:n=2018时不满足条件n≤2017,退出循环,输出S的值为$\frac{\sqrt{3}}{2}$.
解答 解:模拟程序的运行,可得
S=0,n=1
满足条件n≤2017,执行循环体,S=$\frac{\sqrt{3}}{2}$,n=2
满足条件n≤2017,执行循环体,S=$\sqrt{3}$,n=3
满足条件n≤2017,执行循环体,S=$\sqrt{3}$,n=4
满足条件n≤2017,执行循环体,S=$\frac{\sqrt{3}}{2}$,n=5
满足条件n≤2017,执行循环体,S=0,n=6
满足条件n≤2017,执行循环体,S=0,n=7
满足条件n≤2017,执行循环体,S=$\frac{\sqrt{3}}{2}$,n=8
…
观察规律可知,S的取值以6为最小正周期循环,
由于2017=336×6+1,
可得:n=2017时,满足条件n≤2017,执行循环体,S=$\frac{\sqrt{3}}{2}$,n=2018
不满足条件n≤2017,退出循环,输出S的值为$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题主要考查了循环结构的程序框图的应用,正确依次写出前几次循环得到的S,n的值,观察规律可知S的取值以6为最小正周期循环是解题的关键,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.已知递增数列{an}对任意n∈N*均满足an∈N*,aan=3n,记${b_n}={a_{2•{3^{n-1}}}}$(n∈N*),则数列{bn}的前n项和等于( )
| A. | 2n+n | B. | 2n+1-1 | C. | $\frac{{{3^{n+1}}-3n}}{2}$ | D. | $\frac{{{3^{n+1}}-3}}{2}$ |
4.已知实数x,y满足条件$\left\{\begin{array}{l}{3x+y-7≥0}\\{x+3y-13≤0}\\{x-y-1≤0}\end{array}\right.$,则z=|2x+y|的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
11.已知直线m,n与平面α,β,γ满足α⊥β,α∩β=m,n⊥α,n?γ,则下列判断一定正确的是( )
| A. | m∥γ,α⊥γ | B. | n∥β,α⊥γ | C. | β∥γ,α⊥γ | D. | m⊥n,α⊥γ |
 社区服务是综合实践活动课程的重要内容.上海市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段[65,70),[70,75),[75,80),[80,85),[85,90)(单位:小时)进行统计,其频率分布直方图如图所示.
社区服务是综合实践活动课程的重要内容.上海市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段[65,70),[70,75),[75,80),[80,85),[85,90)(单位:小时)进行统计,其频率分布直方图如图所示.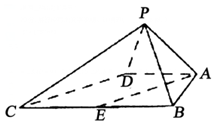 如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.