题目内容
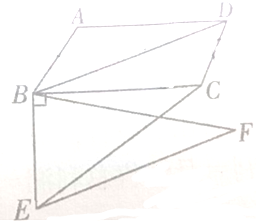 如图,在?ABCD中,AB=
如图,在?ABCD中,AB=| 2 |
考点:三角形的面积公式
专题:解三角形
分析:S平行四边形ABCD=AB•BC•sin45°.在△ABD中,由余弦定理可得BD2=AB2+AD2-2AB•ADcos135°.在△ABD中,由正弦定理可得
=
,可得sin∠ADB=
,于是可得cos∠ADB.因此点D到直线BE的距离h=BDcos∠ADB=4.由于四边形BEFD为平行四边形,可得D与F到直线BE的距离相等.可得△BEF的面积S△BEF=
BE•h即可.
| AB |
| sin∠ADB |
| BD |
| sinA |
| ABsinA |
| BD |
| 1 |
| 2 |
解答:
解:S平行四边形ABCD=AB•BC•sin45°=
×3×
=3.
在△ABD中,由余弦定理可得BD2=AB2+AD2-2AB•ADcos135°=(
)2+32-2×
×3×(-
)=17,
∴BD=
.
在△ABD中,由正弦定理可得
=
,
∴sin∠ADB=
=
=
,
∴cos∠ADB=
.
∴点D到直线BE的距离h=BDcos∠ADB=4.
∵四边形BEFD为平行四边形,∴D与F到直线BE的距离相等.
∴△BEF的面积S△BEF=
BE•h=
×2×4=4.
∴平行四边形ABCD与△BEF的面积之比为3:4.
故答案为:3:4.
| 2 |
| ||
| 2 |
在△ABD中,由余弦定理可得BD2=AB2+AD2-2AB•ADcos135°=(
| 2 |
| 2 |
| ||
| 2 |
∴BD=
| 17 |
在△ABD中,由正弦定理可得
| AB |
| sin∠ADB |
| BD |
| sinA |
∴sin∠ADB=
| ABsinA |
| BD |
| ||
|
| ||
| 17 |
∴cos∠ADB=
4
| ||
| 17 |
∴点D到直线BE的距离h=BDcos∠ADB=4.
∵四边形BEFD为平行四边形,∴D与F到直线BE的距离相等.
∴△BEF的面积S△BEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴平行四边形ABCD与△BEF的面积之比为3:4.
故答案为:3:4.
点评:本题综合考查了三角形的正弦定理、余弦定理、平行四边形的面积、三角形的面积计算公式,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
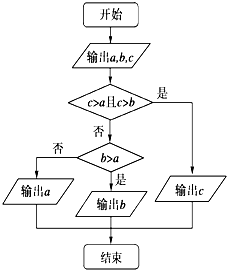 如图程序框图表示的算法是( )
如图程序框图表示的算法是( )| A、将a、b、c按从小到大输出 |
| B、将a、b、c按从大到小输出 |
| C、输出a、b、c三数中的最大数 |
| D、输出a、b、c三数中的最小数 |
 如图所示,已知四棱锥P-ABCD的底面是菱形,∠DAB=
如图所示,已知四棱锥P-ABCD的底面是菱形,∠DAB=