题目内容
 如图所示,已知四棱锥P-ABCD的底面是菱形,∠DAB=
如图所示,已知四棱锥P-ABCD的底面是菱形,∠DAB=| π |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅰ)求证:B、E、C、F四点共面;
(Ⅱ)求直线EP与平面BECF所成角的正弦值;
(Ⅲ)求平面BECF与平面ABCD所成锐二面角的大小.
考点:与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系,点、线、面间的距离计算
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)设PO,BG交点为H,证明H,F,E三点共线,FE∩BG=H,即可证明:B、E、C、F四点共面;
(Ⅱ)∠PEG即为所求,求出PG,PE,即可求直线EP与平面BECF所成角的正弦值;
(Ⅲ)判断∠GBD就是所求二面角的平面角,即可求平面BECF与平面ABCD所成锐二面角的大小.
(Ⅱ)∠PEG即为所求,求出PG,PE,即可求直线EP与平面BECF所成角的正弦值;
(Ⅲ)判断∠GBD就是所求二面角的平面角,即可求平面BECF与平面ABCD所成锐二面角的大小.
解答:
(Ⅰ)证明:设PO,BG交点为H,则
∵O,G分别为BD,PD中点,
∴H为△PBD的重心,
∴OH=
OP
∵CE=
CP,
∴HE∥OC,
同理HF∥OA,
∴H,F,E三点共线,FE∩BG=H
∴B、E、C、F四点共面;
(Ⅱ)解:由题意,PO⊥AC,BD⊥AC,
∴AC⊥平面PBD,
∴AC⊥PD,
∴PD⊥EF,
∵PD⊥BG,
∴PD⊥平面BEGF,
∴∠PEG即为所求,
在直角△PEG中,PG=3,PE=2
,∠PGE=
,
∴直线EP与平面BECF所成角的正弦值为
=
;
(Ⅲ)解:设平面BECF∩平面ABCD=l,
∵EF∥AC,∴EF∥l,
∴∠GBD就是所求二面角的平面角,
在等边三角形ABD中,G为中点,∴∠GBD=30°.
∵O,G分别为BD,PD中点,
∴H为△PBD的重心,
∴OH=
| 1 |
| 3 |
∵CE=
| 1 |
| 3 |
∴HE∥OC,
同理HF∥OA,
∴H,F,E三点共线,FE∩BG=H
∴B、E、C、F四点共面;
(Ⅱ)解:由题意,PO⊥AC,BD⊥AC,
∴AC⊥平面PBD,
∴AC⊥PD,
∴PD⊥EF,
∵PD⊥BG,
∴PD⊥平面BEGF,
∴∠PEG即为所求,
在直角△PEG中,PG=3,PE=2
| 6 |
| π |
| 2 |
∴直线EP与平面BECF所成角的正弦值为
| PG |
| PE |
| ||
| 4 |
(Ⅲ)解:设平面BECF∩平面ABCD=l,
∵EF∥AC,∴EF∥l,
∴∠GBD就是所求二面角的平面角,
在等边三角形ABD中,G为中点,∴∠GBD=30°.
点评:本题考查与二面角有关的立体几何综合,考查空间角,正确找出空间角是关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目

 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.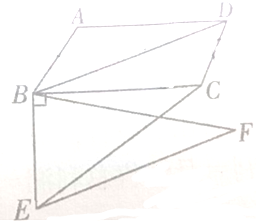 如图,在?ABCD中,AB=
如图,在?ABCD中,AB=