题目内容
对于下列表格所示五个散点，已知求得的线性回归直线方程为
=0.8x-155，则实数m的值为（ ）
 |
| y |
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A、8 | B、8.2 |
| C、8.4 | D、8.5 |
考点：线性回归方程
专题：计算题,概率与统计
分析：根据回归直线经过样本数据中心点，求出y的平均数，进而可求出t值．
解答：
解：由题意，
=
（196+197+200+203+204）=200，
=
（1+3+6+7+m）=
，
代入
=0.8x-155，可得
=0.8×200-155，m=8，
故选：A．
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
| 17+m |
| 5 |
代入
|
| y |
| 17+m |
| 5 |
故选：A．
点评：本题考查线性回归方程的求法和应用，是一道中档题，这种题目解题的关键是求出平均数，代入回归直线方程，注意数字的运算不要出错．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
已知a＞0，且a≠1，则函数f（x）=ax+（x-1）2-2a的零点个数为（ ）
| A、1 | B、2 | C、3 | D、与a有关 |
用1，2，3，4这四个数字，组成比2 000大且无重复数字的四位数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知扇形的面积为2，扇形圆心角的弧度数是4，则扇形的周长为（ ）
| A、6 | ||
B、6
| ||
| C、10 | ||
| D、12 |
甲、乙、丙三人站成一排，则甲、乙相邻的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知某几何体的三视图如图，其中正（主）视图中半圆的半径为1，则该几何体的体积为（ ）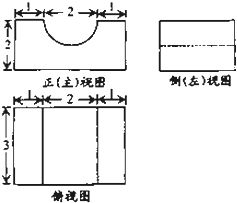
A、24-
| ||||
B、24-
| ||||
| C、24-π | ||||
D、24-
|