题目内容

已知向量
a
=(cosx，sinx)，
b
=(cosy，siny)，若y=x+
7
6
π，则向量
a
与(
a
+
b
)的夹角等于
 
．
考点：数量积表示两个向量的夹角,两角和与差的正弦函数
专题：平面向量及应用
分析：由题意易得|
a
|，|
a
+
b
|和
a
•(
a
+
b
)，由向量的夹角公式易得
a
与(
a
+
b
)的夹角的余弦值，再由反三角函数可得．
解答： 解：∵
a
=(cosx，sinx)，
b
=(cosy，siny)，且y=x+
7
6
π，
∴|
a
|=
cos2x+sin2x
=1，
∴|
a
+
b
|=
(cosx+cosy)2+(sinx+siny)2

=
2+2cos(y-x)
=
2+2cos
7π
6
=
2-
3

∴
a
•(
a
+
b
)=cosx（cosx+cosy）+sinx（sinx+siny）
=1+cos（y-x）=1+cos
7π
6
=1-
3
2
，
∴向量
a
与(
a
+
b
)的夹角的余弦值=
a
•(
a
+
b
)
|
a
||
a
+
b
|
=
2-
3
2
=
3
-1
2
2
=
6
-
2
4
，
∴向量
a
与(
a
+
b
)的夹角等于arccos
6
-
2
4

故答案为：arccos
6
-
2
4
点评：本题考查数量积与向量的夹角，涉及两角和与差的三角函数公式以及反三角函数∴，属中档题．
练习册系列答案
相关题目
椭圆E：
x2
a2
+
y2
3
=1的右焦点为F，直线y=x+m与椭圆E交于A，B两点，若△FAB周长的最大值是8，则m的值等于（　　）
A、0
B、1
C、
3
D、2
三棱柱的三视图如图所示，则该棱柱的体积等于
 
某企业生产A，B两种产品，根据市场调查与预测，A产品的利润与投资关系如图（1）所示；B产品的利润与投资的算术平方根成正比，其关系如图（2）所示（注：利润和投资单位：万元）．

（1）分别将A，B两种产品的利润表示为投资的函数关系式；
（2）已知该企业已筹集到18万元资金，并将全部投入A，B两种产品的生产．问怎样分配这18万元投资，才能使该企业获得最大利润？其最大利润约为多少万元？
已知A（-1，-3），B（1，1）求直线AB与直线x+y-5=0的交点C的坐标．
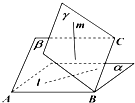如图，二面角α-AB-β与β-BC-γ均为θ（0＜θ＜π），AB⊥BC，l?α，m?γ，则下列不可能成立的是（　　）
A、l∥mB、l⊥m
C、m∥ABD、α⊥γ
若直线l：y=（a+1）x-1与曲线C：y2=ax恰好有一个公共点，试求实数a的取值集合，并指出a=0，a=-1时a的几何意义．
已知函数f（x）=x（x-1）2．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若对于任意的x∈（0，+∞），f（x）≥ax2恒成立，求实数a的取值范围．
已知周期为4的函数f（x）=
m
1-x2
，(-1≤x≤1)
1-|x-2|，(1＜x≤3)
，其中m＞0，若关于x的方，3f（x）=x恰有5个不同实数解，则m的取值范围是（　　）
A、（
15
3
，
7
）
B、（
4
3
，
7
）
C、（
4
3
，
5
3
）
D、（
15
3
，3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网