Question

某企业生产A，B两种产品，根据市场调查与预测，A产品的利润与投资关系如图（1）所示；B产品的利润与投资的算术平方根成正比，其关系如图（2）所示（注：利润和投资单位：万元）．

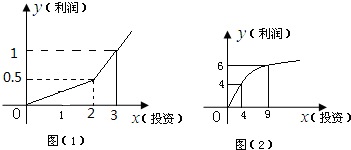
（1）分别将A，B两种产品的利润表示为投资的函数关系式；
（2）已知该企业已筹集到18万元资金，并将全部投入A，B两种产品的生产．问怎样分配这18万元投资，才能使该企业获得最大利润？其最大利润约为多少万元？

Answer 1

考点：函数模型的选择与应用

专题：函数的性质及应用

分析：（1）对于A，当0≤x≤2时，因为图象过（2，0.5）和原点，当x＞2时，图象过（2，0.5）和（3，1），可得函数的解析式；对于B，易知y=2

x

(x≥0)．
（2）设投入B产品x万元，则投入A产品（18-x）万元，利润为y万元．分16≤x≤18时，0≤x＜16时两种情况求出函数的最大值，比较后可得答案．

解答： 解：（1）对于A，当0≤x≤2时，因为图象过（2，0.5），所以y=

1

2

x，…2分
当x＞2时，令y=kx+b，因图象过（2，0.5）和（3，1），得

1 2 =2k+b 1=3k+b

，
解得k=

1

2

，b=-

1

2

，故y=

1 2 x，0≤x≤2 1 2 x- 1 2 ，x＞2

；…4分
对于B，易知y=2

x

(x≥0)．…5分
（2）设投入B产品x万元，则投入A产品（18-x）万元，利润为y万元．
若16≤x≤18时，则0≤18-x≤2，则投入A产品的利润为

1

2

(18-x)，投入B产品的利润为2

x

，则y=

1

2

(18-x)+2

x

，令

x

=t，t∈[4，3

2

]，
则y=-

1

2

t2+2t+9，此时当t=4，即x=16时，y_max=9万元；…8分
当0≤x＜16时，2＜18-x≤18，则投入A产品的利润为

1

2

(18-x)-

1

2

，投入B产品的利润为2

x

，则y=

1

2

(18-x)+2

x

-

1

2

，令

x

=t，t∈[0，4），
则y=-

1

2

t2+2t+

17

2

，当t=2时，即x=4时，y_max=10.5万元；…11分
由10.5＞9，
综上，投入A产品14万元，B产品4万元时，总利润最大值为10.5万元．…12分．

点评：本题考查的知识点是函数的选择与应用，函数的最值，难度不大，属于基础题．