题目内容
已知函数f(x)=x(x-1)2.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若对于任意的x∈(0,+∞),f(x)≥ax2恒成立,求实数a的取值范围.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若对于任意的x∈(0,+∞),f(x)≥ax2恒成立,求实数a的取值范围.
考点:利用导数研究函数的单调性,函数恒成立问题
专题:计算题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)求导f′(x)=2x(x-1)+(x-1)2=(x-1)(3x-1),利用导数的正负确定函数的单调性;
(Ⅱ)对x∈(0,+∞),f(x)≥ax2可化为a≤
=
,从而令F(x)=
=(1-
)2,化恒成立问题为最值问题.
(Ⅱ)对x∈(0,+∞),f(x)≥ax2可化为a≤
| x(x-1)2 |
| x2 |
| (x-1)2 |
| x |
| (x-1)2 |
| x2 |
| 1 |
| x |
解答:
解:(Ⅰ)f′(x)=2x(x-1)+(x-1)2=(x-1)(3x-1),
故当x∈(-∞,
),(1,+∞)时,f′(x)>0;
当x∈(
,1)时,f′(x)<0;
故函数f(x)的单调增区间为(-∞,
),(1,+∞);
单调减区间为(
,1);
(Ⅱ)∵x∈(0,+∞),
∴f(x)≥ax2可化为a≤
=
=x+
-2,
∵x+
≥2,当x=
时取等号,
即x=1时,
取得最小值,
∴a≤2-2=0
故a≤0.
故当x∈(-∞,
| 1 |
| 3 |
当x∈(
| 1 |
| 3 |
故函数f(x)的单调增区间为(-∞,
| 1 |
| 3 |
单调减区间为(
| 1 |
| 3 |
(Ⅱ)∵x∈(0,+∞),
∴f(x)≥ax2可化为a≤
| x(x-1)2 |
| x2 |
| (x-1)2 |
| x |
| 1 |
| x |
∵x+
| 1 |
| x |
| 1 |
| x |
即x=1时,
| x(x-1)2 |
| x2 |
∴a≤2-2=0
故a≤0.
点评:本题考查了导数在判断函数的单调性中的应用及恒成立问题化为最值问题的处理方法,属于中档题.

练习册系列答案
相关题目
计算
(1+
)dx的结果为( )
| ∫ | 1 0 |
| 1-x2 |
| A、1 | ||
B、
| ||
C、1+
| ||
D、1+
|
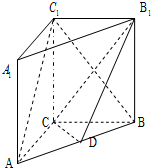 如图,在三棱柱ABC-A1B1C1中,侧棱A1A垂直于底面ABC,AC=3,BC=4,AB=5,AA1=4点D是AB的中点,
如图,在三棱柱ABC-A1B1C1中,侧棱A1A垂直于底面ABC,AC=3,BC=4,AB=5,AA1=4点D是AB的中点,