题目内容
若直线l：y=（a+1）x-1与曲线C：y2=ax恰好有一个公共点，试求实数a的取值集合，并指出a=0，a=-1时a的几何意义．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：联立方程组，消去y得到关于x的准一元二次方程，分二次项的系数等于零和不为零两种情况进行讨论．
解答：
解：联立方程组
，得：（a+1）2x2-（3a+2）x+1=0．
当a=-1时，显然成立；
当a≠-1时，由△=（3a+2）2-4（a+1）2=0，解得a=0或-
．
综上，a=0、-1、-
．
则实数a的取值集合为{0，-1，-
}．
当a=0时，曲线C为x轴，两直线有一个交点；
a=-1时直线l平行于抛物线的对称轴，与抛物线有一个交点．
|
当a=-1时，显然成立；
当a≠-1时，由△=（3a+2）2-4（a+1）2=0，解得a=0或-
| 4 |
| 5 |
综上，a=0、-1、-
| 4 |
| 5 |
则实数a的取值集合为{0，-1，-
| 4 |
| 5 |
当a=0时，曲线C为x轴，两直线有一个交点；
a=-1时直线l平行于抛物线的对称轴，与抛物线有一个交点．
点评：本题考查了抛物线的简单几何性质，考查了由一元二次方程的判别式判断根的个数问题，是基础题．
练习册系列答案
相关题目
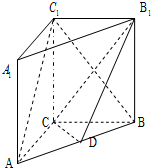如图，在三棱柱ABC-A1B1C1中，侧棱A1A垂直于底面ABC，AC=3，BC=4，AB=5，AA1=4点D是AB的中点，