题目内容
若集合M={x|x2+x-2xλ≥0,x∈N*},若集合M中的元素个数为4,则实数λ的取值范围为 .
考点:函数恒成立问题
专题:集合
分析:可对x=1,2,3,4,5进行分析求出λ的取值范围,研究当x≥6时,不等式恒成立转化为求函数的最值,从而求出λ的取值范围,根据集合M中的元素个数为4,确定λ的取值范围.
解答:
解:集合M={x|x2+x-2xλ≥0,x∈N*},
x=1时,2-2λ≥0,解得λ≤1,
x=2时,6-4λ≥0,解得λ≤
,
x=3时,12-8λ≥0,解得λ≤
,
x=4时,20-16λ≥0,解得λ≤
,
x=5时,30-32λ≥0,解得λ≤
,
由x2+x-2xλ≥0得λ≤
,
若x≥6时,x2+x-2xλ≥0恒成立,则
λ≤
恒成立,
令f(x)=
,则当x≥6时,f(x)≥
,
∴λ≤
.
∵集合M中的元素个数为4,
∴
<λ≤1.
故答案为:(
,1].
x=1时,2-2λ≥0,解得λ≤1,
x=2时,6-4λ≥0,解得λ≤
| 3 |
| 2 |
x=3时,12-8λ≥0,解得λ≤
| 3 |
| 2 |
x=4时,20-16λ≥0,解得λ≤
| 5 |
| 4 |
x=5时,30-32λ≥0,解得λ≤
| 15 |
| 16 |
由x2+x-2xλ≥0得λ≤
| x2+x |
| 2x |
若x≥6时,x2+x-2xλ≥0恒成立,则
λ≤
| x2+x |
| 2x |
令f(x)=
| x2+x |
| 2x |
| 21 |
| 32 |
∴λ≤
| 21 |
| 32 |
∵集合M中的元素个数为4,
∴
| 15 |
| 16 |
故答案为:(
| 15 |
| 16 |
点评:本题以集合中元素的个数为载体,考查不等式的恒成立问题,转化为求函数的最值问题,通过列举加以分析最后确定范围,值得借鉴.

练习册系列答案
相关题目
若复数z满足z(1+i)=i(i为虚数单位),则z为( )
A、
| ||
B、
| ||
| C、1+i | ||
| D、1-i |
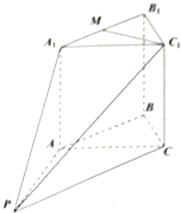 如图所示,在正三棱柱(底面是正三角形的直棱柱)A1B1C1-ABC中,M为A1B1的中点,P∈平面ABC,PA⊥平面ACC1A1,且AB=AA1=4,PA=4
如图所示,在正三棱柱(底面是正三角形的直棱柱)A1B1C1-ABC中,M为A1B1的中点,P∈平面ABC,PA⊥平面ACC1A1,且AB=AA1=4,PA=4