Question

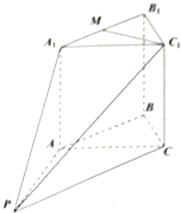如图所示，在正三棱柱（底面是正三角形的直棱柱）A₁B₁C₁-ABC中，M为A₁B₁的中点，P∈平面ABC，PA⊥平面ACC₁A₁，且AB=AA₁=4，PA=4

3

．
（1）求证：C₁M⊥平面PCC₁；
（2）求二面角A₁-PC₁-C的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面垂直的判定

专题：空间角

分析：（1）以A为原点，建立空间直角坐标系A-xyz，利用向量法能证明C₁M⊥平面PCC₁．
（2）分别求出平面A₁PC₁的法向量和平面PC₁C的法向量，利用向量法能求出二面角A₁-PC₁-C的余弦值．

解答： （1）证明：以A为原点，建立空间直角坐标系A-xyz，如图所示，
则P（4

3

，0，0），M（-

3

，1，4），A₁（0，0，4），C₁（0，4，4），
∴

C1M

=（-

3

，-3，0），

CC1

=（0，0，4），

PC

（-4

3

，4，0），
∵

C1M

•

CC1

=0，

C1M

•

PC

=0，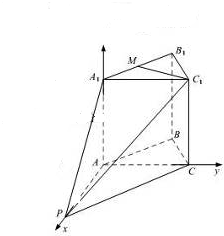
∴C₁M⊥CC₁，C₁M⊥PC，
∵CC₁∩PC=C，CC₁?平面PCC₁，PC?平面PCC₁，
∴C₁M⊥平面PCC₁．
（2）

A1C1

=（0，4，0），

A1P

=（4

3

，0，-4），
设平面A₁PC₁的法向量

n

=（x，y，z），
则

n • A1C1 =4y=0 n • A1P =4 3 x-4z=0

，取x=1，得

n

=（1，0，

3

），
由（1）知平面PC₁C的一个法向量为

C1M

=（-

3

，-3，0），
∴cos＜

C1M

，

n

＞=

- 3

2×2 3

=-

1

4

，
∴二面角A₁-PC₁-C的余弦值为-

1

4

．

点评：本题考查空间点、线、面位置关系，考查二面角、空间向量及坐标运算等基础知识，考查空间想象能力、运算能力和推理论证能力，考查用向量方法解决问题能力．