题目内容
现有两只口袋A,B,口袋A中装着编号分别为1,3,5,7,9的五个形状完全相同的小球,口袋B中装着编号分别为2,4,6,8的四个形状完全相同的小球,某人先从口袋A中随机摸出一小球,记编号为a,然后从口袋B中摸小球,若所得小球的编号为2a,则停止,否则再从口袋B中剩余的小球中摸一球,将从口袋B中所得小球的编号相加,若和为2a,则停止,否则一直摸下去,直到和为2a为止,或者直到小球摸完为停止.
(1)求此人只摸两次的概率;
(2)若此人摸小球的次数X与所得奖金的函数关系为Y=100(5-X),求奖金Y的分布列与期望.
(1)求此人只摸两次的概率;
(2)若此人摸小球的次数X与所得奖金的函数关系为Y=100(5-X),求奖金Y的分布列与期望.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)设从A中摸到编号的小球为Ai(i=1,3,5,7,9),从B中摸到的小球的编号为Bi(i=2,4,6,8),
此人只摸两次的概率.
(2)X可能出现的值为2,3,4,5,η可能出现的值为300,200,100,0,分别求出相应的概率,由此能求出奖金Y的分布列与期望.
此人只摸两次的概率.
(2)X可能出现的值为2,3,4,5,η可能出现的值为300,200,100,0,分别求出相应的概率,由此能求出奖金Y的分布列与期望.
解答:
解:(1)设从A中摸到编号的小球为Ai(i=1,3,5,7,9),
从B中摸到的小球的编号为Bi(i=2,4,6,8),
此人只摸两次的概率为:
p=P(A1B2+A3B4)=P(A1B2)+P(A3B4)
=
×
+
×
=
.
(2)X可能出现的值为2,3,4,5,
P(X=2)=P(A1B2+A3B4)=
×
×2=
,
P(X=3)=P(2A1B2B4+2A3B2B6+2A5B4B6+2A7B6B8)
=4×2×
×
×
=
,
P(ξ=4)=P(6A7B2B4B6+6A9B4B6B8)
=6×2×
×
×
×
=
,
P(ξ=5)=1-(
+
+
)=
,
由题意知η可能出现的值为300,200,100,0,其分布列为:
Eη=300×
+200×
+100×
=
.
从B中摸到的小球的编号为Bi(i=2,4,6,8),
此人只摸两次的概率为:
p=P(A1B2+A3B4)=P(A1B2)+P(A3B4)
=
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 10 |
(2)X可能出现的值为2,3,4,5,
P(X=2)=P(A1B2+A3B4)=
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 10 |
P(X=3)=P(2A1B2B4+2A3B2B6+2A5B4B6+2A7B6B8)
=4×2×
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
| 2 |
| 15 |
P(ξ=4)=P(6A7B2B4B6+6A9B4B6B8)
=6×2×
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 10 |
P(ξ=5)=1-(
| 1 |
| 10 |
| 2 |
| 15 |
| 1 |
| 10 |
| 2 |
| 3 |
由题意知η可能出现的值为300,200,100,0,其分布列为:
| η | 300 | 200 | 100 | 0 | ||||||||
| P |
|
|
|
|
| 1 |
| 10 |
| 2 |
| 15 |
| 1 |
| 10 |
| 200 |
| 3 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
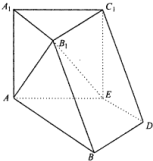 如图,在六面体A1B1C1-ABDE中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AA1⊥AB,四边形AEC1A1是正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1-ABDE中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AA1⊥AB,四边形AEC1A1是正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.