Question

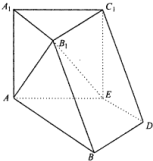如图，在六面体A₁B₁C₁-ABDE中，平面A₁B₁C₁∥平面ABDE，△A₁B₁C₁是正三角形，四边形AA₁B₁B是直角梯形，AA₁⊥AB，四边形AEC₁A₁是正方形，四边形ABDE是等腰梯形，AB∥DE，AB=2AE=2DE=2．
（Ⅰ）证明：AB₁∥平面C₁DE；
（Ⅱ）求平面AB₁E与平面BB₁C₁D所成锐二面角的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题,平面与平面平行的判定

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）证明AB₁∥平面C₁DE，通过证明平面ABB₁A₁∥平面C₁DE即可；
（Ⅱ）延长AE，BD交于点P，连接B₁P交C₁D于Q，则B₁P为平面AB₁E与平面BB₁C₁D的交线，作BH⊥B₁P于H，则AH⊥BH，可得∠ABH为平面AB₁E与平面BB₁C₁D所成锐二面角，即可求平面AB₁E与平面BB₁C₁D所成锐二面角的余弦值．

解答： （Ⅰ）证明：∵四边形AEC₁A₁是正方形，
∴AA₁∥EC₁，
∵AA₁?平面C₁DE，EC₁?平面C₁DE，
∴AA₁∥平面C₁DE；
同理AB∥平面C₁DE；
∵AB∩AA₁=A
∴平面ABB₁A₁∥平面C₁DE
∴AB₁∥平面C₁DE；
（Ⅱ）解：延长AE，BD交于点P，连接B₁P交C₁D于Q，则B₁P为平面AB₁E与平面BB₁C₁D的交线，
∵四边形ABDE是等腰梯形，AB∥DE，AB=2AE=2DE=2，
∴AP=BP=2，AB₁=BB₁=

2

，B₁P=2，
△AB₁P≌△BB₁P，作BH⊥B₁P于H，
则AH⊥BH，∴∠ABH为平面AB₁E与平面BB₁C₁D所成锐二面角．
∵BH=AH=

7

2

，∴cos∠AHB=

1

7

，
∴平面AB₁E与平面BB₁C₁D所成锐二面角的余弦值为

1

7

．

点评：本题考查直线与平面的平行，二面角的求法等知识，考查空间想象能力，逻辑思维能力，是中档题．