题目内容
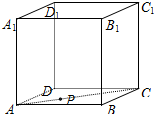 如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题:
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题:①D1P∥平面A1BC1
②D1P⊥BD
③平面PDB1⊥平面A1BC1
④三棱锥A1-BPC1的体积不变.
则其中所以正确的命题的序号是
考点:命题的真假判断与应用
专题:证明题,空间位置关系与距离
分析:利用面面平行的判定定理与性质定理,面面垂直的判定定理与三棱锥体积轮换公式对①②③④四个选项逐一分析判断即可.
解答:
解:①,在正方体ABCD-A1B1C1D1中,D1A∥C1B,D1A?平面A1BC1,C1B?平面A1BC1,
∴D1A∥平面A1BC1,
同理可证,D1C∥平面A1BC1,D1A∩D1C=D1,
∴平面D1AC∥平面A1BC1,又D1P?平面D1AC,
∴D1P∥平面A1BC1,故①正确;
②,当点P为AC与BD的交点时,BD⊥平面BDD1,D1P?平面BDD1,这时,D1P⊥BD,除此之外,D1P不与BD垂直,故②错误;
③,∵DB1在平面A1B1C1D1上的射影为B1D1,B1D1⊥A1C1(正方形的两条对角线互相垂直),
DB1在平面BB1C1C的射影为B1C,B1C⊥BC1(正方形的两条对角线互相垂直),
由三垂线定理的逆定理可知,B1D⊥A1C1,B1D⊥BC1,A1C1∩BC1=C1,
∴B1D⊥平面A1BC1,B1D?平面PDB1,
∴平面PDB1⊥平面A1BC1,故③正确;
④,设正方体的边长为1,点B到平面A1BC1的距离就是点B到平面A1ACC1的距离,为
BD=
,S△A1PC1=
A1C1•h=
×
×1=
,
∵VA1-BPC1=VB-A1PC1=
S△A1PC1•
BD=
×(
)2=
,为定值,故④正确.
故答案为:①③④.
∴D1A∥平面A1BC1,
同理可证,D1C∥平面A1BC1,D1A∩D1C=D1,
∴平面D1AC∥平面A1BC1,又D1P?平面D1AC,
∴D1P∥平面A1BC1,故①正确;
②,当点P为AC与BD的交点时,BD⊥平面BDD1,D1P?平面BDD1,这时,D1P⊥BD,除此之外,D1P不与BD垂直,故②错误;
③,∵DB1在平面A1B1C1D1上的射影为B1D1,B1D1⊥A1C1(正方形的两条对角线互相垂直),
DB1在平面BB1C1C的射影为B1C,B1C⊥BC1(正方形的两条对角线互相垂直),
由三垂线定理的逆定理可知,B1D⊥A1C1,B1D⊥BC1,A1C1∩BC1=C1,
∴B1D⊥平面A1BC1,B1D?平面PDB1,
∴平面PDB1⊥平面A1BC1,故③正确;
④,设正方体的边长为1,点B到平面A1BC1的距离就是点B到平面A1ACC1的距离,为
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
∵VA1-BPC1=VB-A1PC1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| ||
| 2 |
| 1 |
| 12 |
故答案为:①③④.
点评:本题考查空间直线与平面、平面与平面的位置关系及体积,突出考查面面平行的判定定理与性质定理,考查面面垂直的判定定理,考查几何体的体积运算,属于难题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
在(a+b)n展开式中,若第14项与第15项的二项式系数之比为1:2,则二项式系数最大的项是( )
| A、第17项 |
| B、第18项 |
| C、第20项或第21项 |
| D、第21项或第22项 |
已知命题p:“?x∈R,|x|+x2>0“,命题q:“a+c>b+d“是a>b且c>d的充分不必要条件”,则下列结论正确的是( )
| A、命题“p∧q”是真命题 |
| B、命题“(¬p)∧q”是真命题 |
| C、命题“p∧(-q)”是真命题 |
| D、命题“p∨q”是假命题 |
数列{an}满足:a1=1,a2=2,an=
(n≥3且n∈N),则a2014=( )
| an-1 |
| an-2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、2-2014 |
已知数列{an}是递增等差数列,若a2014+a2015<0,a2014•a2015<0,且数列{an}的前n项和Sn有最小值,那么Sn取得最小正值时n等于( )
| A、4029 | B、4028 |
| C、4027 | D、4026 |
若圆C1:x2+y2-2x=0与直线l:y-mx-m=0有两个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|