题目内容
在（a+b）n展开式中，若第14项与第15项的二项式系数之比为1：2，则二项式系数最大的项是（ ）
| A、第17项 |
| B、第18项 |
| C、第20项或第21项 |
| D、第21项或第22项 |
考点：二项式系数的性质
专题：二项式定理
分析：由条件利用组合数的计算公式、二项式系数的定义求出n=41，再利用二项式系数的性质可得二项式系数最大的项．
解答：
解：由题意可得
=
•
=
=
，∴n=41．
再根据二项式系数的性质可得，第21项或第22项的二项式系数最大，
故选：D．
| ||
|
| n! |
| 13!(n-13)! |
| 14!(n-14)! |
| n! |
| 14 |
| n-13 |
| 1 |
| 2 |
再根据二项式系数的性质可得，第21项或第22项的二项式系数最大，
故选：D．
点评：本题主要考查二项式系数的定义、性质，组合数的计算公式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数y=sin（
x-
）的最小正周期是（ ）
| 1 |
| 2 |
| π |
| 10 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
已知集合B={2，3，4}，那么B的真子集的个数是（ ）
| A、15 | B、16 | C、7 | D、8 |
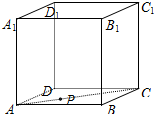如图，在正方体ABCD-A1B1C1D1中，点P在面对角线AC上运动，给出下列命题：