题目内容
f(x)=x2+ex-
(x<0),g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点,则a的取值范围是 .
| 1 |
| 2 |
考点:根的存在性及根的个数判断,函数的图象
专题:计算题,函数的性质及应用
分析:由题意可得,存在x<0使f(x)-g(-x)=0,即ex-
-ln(-x+a)=0在(-∞,0)上有解,从而化为函数m(x)=ex-
-ln(-x+a)在(-∞,0)上有零点,从而求解.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由题意,存在x<0,
使f(x)-g(-x)=0,
即ex-
-ln(-x+a)=0在(-∞,0)上有解,
令m(x)=ex-
-ln(-x+a),
则m(x)=ex-
-ln(-x+a)在其定义域上是增函数,
且x→-∞时,m(x)<0,
则ex-
-ln(-x+a)=0在(-∞,0)上有解可化为
e0-
-ln(a)>0,
即lna<
,
故a<
.
故答案为:(-∞,
).
使f(x)-g(-x)=0,
即ex-
| 1 |
| 2 |
令m(x)=ex-
| 1 |
| 2 |
则m(x)=ex-
| 1 |
| 2 |
且x→-∞时,m(x)<0,
则ex-
| 1 |
| 2 |
e0-
| 1 |
| 2 |
即lna<
| 1 |
| 2 |
故a<
| e |
故答案为:(-∞,
| e |
点评:本题考查了函数的图象与方程的根及函数的零点之间的关系,属于中档题.

练习册系列答案
相关题目
已知集合B={2,3,4},那么B的真子集的个数是( )
| A、15 | B、16 | C、7 | D、8 |
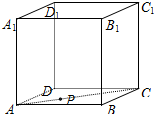 如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题:
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题: