题目内容
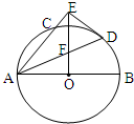如图，AB是☉O的直径，AC是弦，∠BAC的平分线AD交☉O于点D，DE⊥AC，交AC的延长线于点E，OE交AD于点F．（Ⅰ）求证：DE 是☉O的切线；
（Ⅱ）若
| AC |
| AB |
| 2 |
| 5 |
| AF |
| DF |
考点：与圆有关的比例线段,圆的切线的判定定理的证明
专题：立体几何
分析：（Ⅰ）连结OD，由圆的性质得OD∥AE，由AE⊥DE，得DE⊥OD，由此能证明DE是⊙O切线．
（Ⅱ）过D作DH⊥AB于H，则有cos∠DOH=cos∠CAB=
=
，设OD=5x，则AB=10x，OH=2x，AH=7x，由已知得△AED≌AHD，△AEF∽△DOF，由此能求出
．
（Ⅱ）过D作DH⊥AB于H，则有cos∠DOH=cos∠CAB=
| AC |
| AB |
| 2 |
| 5 |
| AF |
| DF |
解答：
（Ⅰ）证明：连结OD，由圆的性质得∠ODA=∠OAD=∠DAC，
OD∥AE，又AE⊥DE，∴DE⊥OD，
又OD为半径，∴DE是⊙O切线．
（Ⅱ）解：过D作DH⊥AB于H，则有∠DOH=∠CAB，
cos∠DOH=cos∠CAB=
=
，
设OD=5x，则AB=10x，OH=2x，∴AH=7x，
∵∠BAC的平分线AD交⊙O于点D，DE⊥AC，
DH⊥AB，交AB于H，
∴△AED≌AHD，∴AE=AH=7x，
又OD∥AE，∴△AEF∽△DOF，
∴
=
=
=
=
．
OD∥AE，又AE⊥DE，∴DE⊥OD，
又OD为半径，∴DE是⊙O切线．
（Ⅱ）解：过D作DH⊥AB于H，则有∠DOH=∠CAB，
cos∠DOH=cos∠CAB=
| AC |
| AB |
| 2 |
| 5 |
设OD=5x，则AB=10x，OH=2x，∴AH=7x，
∵∠BAC的平分线AD交⊙O于点D，DE⊥AC，
DH⊥AB，交AB于H，
∴△AED≌AHD，∴AE=AH=7x，
又OD∥AE，∴△AEF∽△DOF，
∴
| AF |
| DF |
| AE |
| OD |
| AH |
| OD |
| 7x |
| 5x |
| 7 |
| 5 |
点评：本题考查圆的切线的证明，考查圆内两线段的比值的求法，是中档题，解题时要认真审题，注意三角形全等和三角形相似的性质的合理运用．
练习册系列答案
教材全解字词句篇系列答案
相关题目
（1+x）2+（1+x）3+（1+x）4+…+（1+x）30的展开式中含x2的系数为（ ）
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
2015°是（ ）
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
如图，EA与圆O相切于点A，D是EA的中点，过点D引圆O的割线，与圆O相交于点B，C，连结EC．