题目内容
 如图,EA与圆O相切于点A,D是EA的中点,过点D引圆O的割线,与圆O相交于点B,C,连结EC.
如图,EA与圆O相切于点A,D是EA的中点,过点D引圆O的割线,与圆O相交于点B,C,连结EC.求证:∠DEB=∠DCE.
考点:与圆有关的比例线段
专题:立体几何
分析:由切割线定理:DA2=DB•DC,从则DE2=DB•DC,进而△EDB~△CDE,由此能证明∠DEB=∠DCE.
解答:
证明:∵EA与⊙O相切于点A.
∴由切割线定理:DA2=DB•DC.
∵D是EA的中点,
∴DA=DE.∴DE2=DB•DC.…(5分)
∴
=
.∵∠EDB=∠CDE,
∴△EDB~△CDE,∴∠DEB=∠DCE…(10分)
∴由切割线定理:DA2=DB•DC.
∵D是EA的中点,
∴DA=DE.∴DE2=DB•DC.…(5分)
∴
| DE |
| DC |
| DB |
| DE |
∴△EDB~△CDE,∴∠DEB=∠DCE…(10分)
点评:本题考查两角相等的证明,是中档题,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
集合A={0,1,2},B={x∈Z|x2<9},则A∩B=( )
| A、{1,2} |
| B、{0,1,2} |
| C、{1,2,3} |
| D、{0,1,2,3} |
设点(3,4)为奇函数y=f(x)图象上的点,则下列各点在函数图象上的是( )
| A、(-3,4) |
| B、(3,-4) |
| C、(-3,-4) |
| D、(-4,-3) |
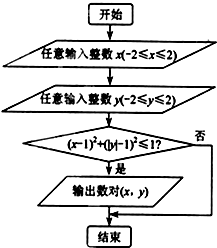 执行如图的程序框图,任意输入一次x(x∈Z,-2≤x≤2)与y(y∈Z,-2≤y≤2),则能输出数对(x,y)的概率为( )
执行如图的程序框图,任意输入一次x(x∈Z,-2≤x≤2)与y(y∈Z,-2≤y≤2),则能输出数对(x,y)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知正△ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB上的中点,过点E作球O的截面,则截面面积的最小值是( )
| A、2π | ||
B、
| ||
| C、3π | ||
D、
|
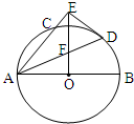 如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.