题目内容
已知数列{an}的通项公式为an=n2cos
(n∈N*),则S3n= .
| 2nπ |
| 3 |
考点:数列的求和
专题:等差数列与等比数列
分析:由已知求出a3n-2+a3n-1+a3n,然后由S3n=(a1+a2+a3)+(a4+a5+a6)+…+(a3n-2+a3n-1+a3n)采用分组求和得答案.
解答:
解:∵an=n2cos
,
∴a3n-2+a3n-1+a3n=-
-
+9n2=
.
∴S3n=(a1+a2+a3)+(a4+a5+a6)+…+(a3n-2+a3n-1+a3n)
=(9-
)+(9×2-
)+…+(9n-
)
=9(1+2+…+n)-
=
.
故答案为:
.
| 2nπ |
| 3 |
∴a3n-2+a3n-1+a3n=-
| (3n-2)2 |
| 2 |
| (3n-1)2 |
| 2 |
| 18n-5 |
| 2 |
∴S3n=(a1+a2+a3)+(a4+a5+a6)+…+(a3n-2+a3n-1+a3n)
=(9-
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
=9(1+2+…+n)-
| 5n |
| 2 |
| 9n2+4n |
| 2 |
故答案为:
| 9n2+4n |
| 2 |
点评:本题考查了数列和的求法,考查了数列的分组求和,是中档题.

练习册系列答案
相关题目
已知定义在R上的偶函数f(x)满足f(x-4)=f(x),且在区间[0,2]上f(x)=x,若关于x的方程f(x)=logax有三个不同的根,则a的范围为( )
| A、(2,4) | ||||
B、(2,2
| ||||
C、(
| ||||
D、(
|
复数
对应的点位于( )
| 1-i |
| 2-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
集合A={0,1,2},B={x∈Z|x2<9},则A∩B=( )
| A、{1,2} |
| B、{0,1,2} |
| C、{1,2,3} |
| D、{0,1,2,3} |
设点(3,4)为奇函数y=f(x)图象上的点,则下列各点在函数图象上的是( )
| A、(-3,4) |
| B、(3,-4) |
| C、(-3,-4) |
| D、(-4,-3) |
已知正△ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB上的中点,过点E作球O的截面,则截面面积的最小值是( )
| A、2π | ||
B、
| ||
| C、3π | ||
D、
|
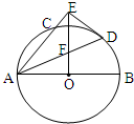 如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.