题目内容
有3名男生,4名女生,在下列不同的要求下,求不同的排列方法总数.
(1)全体排成一行,其中甲不在最左边,乙不在最右边;
(2)全体排成一行,男、女各不相邻;
(3)全体排成一排,其中甲、乙、丙三维同学自左至右的顺序保持不变.
(1)全体排成一行,其中甲不在最左边,乙不在最右边;
(2)全体排成一行,男、女各不相邻;
(3)全体排成一排,其中甲、乙、丙三维同学自左至右的顺序保持不变.
考点:排列、组合及简单计数问题,计数原理的应用
专题:排列组合
分析:(1)利用间接法,先任意排,再排除甲在最左边,乙在最右边,问题得以解决,
(2)利用抽空法,先排3名男生,形成4个空,再将4名女生插入,问题得以解决,
(3)定序排列,先全排列,再除以甲、乙、丙三位同学的顺序,问题得以解决
(2)利用抽空法,先排3名男生,形成4个空,再将4名女生插入,问题得以解决,
(3)定序排列,先全排列,再除以甲、乙、丙三位同学的顺序,问题得以解决
解答:
解:(1)利用间接法,先任意排,再排除甲在最左边,乙在最右边,故有
-2
+
=3760种,
(2)利用抽空法,先排3名男生,形成4个空,再将4名女生插入,故有
•
=144种,
(3)定序排列,先全排列,再除以甲、乙、丙三位同学的顺序,故有
=840种
| A | 7 7 |
| A | 6 6 |
| A | 5 5 |
(2)利用抽空法,先排3名男生,形成4个空,再将4名女生插入,故有
| A | 3 3 |
| A | 4 4 |
(3)定序排列,先全排列,再除以甲、乙、丙三位同学的顺序,故有
| ||
|
点评:本题考查排列、组合及简单计数问题,考查学生的计算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
函数f(x)=
,若f(x)≤a|x|对任意实数x都成立,则实数a的最小值是( )
|
A、
| ||
B、
| ||
| C、6 | ||
| D、4 |
集合A={0,1,2},B={x∈Z|x2<9},则A∩B=( )
| A、{1,2} |
| B、{0,1,2} |
| C、{1,2,3} |
| D、{0,1,2,3} |
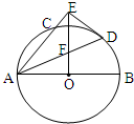 如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.