题目内容
设a＞0，b＞0，a+b=1．
（1）证明：
+
+
≥8；
（2）证明：（a+
）2+（b+
）2≥
．
（1）证明：
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
（2）证明：（a+
| 1 |
| a |
| 1 |
| b |
| 25 |
| 2 |
考点：不等式的基本性质
专题：不等式
分析：（1）利用1的代换把不等式的左边变形后，使用基本不等式可证不等式成立．
（2）把不等式的左边变形后，使用基本不等式可证不等式成立．
（2）把不等式的左边变形后，使用基本不等式可证不等式成立．
解答：
证明：（1）∵a＞0，b＞0，a+b=1，
左边=
+
+
=
+
+
=2+
+
+
+
=2+
+
+
+
=4+2（
+
）≥4+2
=8，当且仅当a=b=
取等号
∴
+
+
≥8成立，
（2）∵ab≤(
)2=
∴（a+
）2+（b+
）2=a2+
+2+2+b2+
=4+（a+b）2-2ab+（
+
）2-
=4+1-2ab+
-
≥5-
+16-8=
，当且仅当a=b=
取等号
∴（a+
）2+（b+
）2≥
成立
左边=
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
| a+b |
| a |
| a+b |
| b |
| a+b |
| ab |
| b |
| a |
| a |
| b |
| 1 |
| b |
| 1 |
| a |
| b |
| a |
| a |
| b |
| a+b |
| a |
| a+b |
| b |
| b |
| a |
| a |
| b |
|
| 1 |
| 2 |
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
（2）∵ab≤(
| a+b |
| 2 |
| 1 |
| 4 |
∴（a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| a |
| 1 |
| b |
| 2 |
| ab |
| 1 |
| (ab)2 |
| 2 |
| ab |
| 1 |
| 2 |
| 25 |
| 2 |
| 1 |
| 2 |
∴（a+
| 1 |
| a |
| 1 |
| b |
| 25 |
| 2 |
点评：本题考查基本不等式的应用，用比较法证明不等式，式子的变形是证明的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
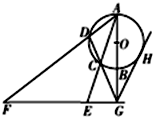如图所示，AB是⊙O的直径，G为AB延长线上的一点，GCD是⊙O的割线，过点G作 AB的垂线，交AC的延长线于点 E，交AD的延长线于点F，过G作⊙O的切线，切点为H，求证：
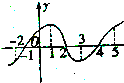如图所示的是函数y=f（x）的导函数y=f′（x）的图象，则[-2，5]上函数f（x）的递增区间为