题目内容
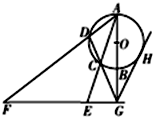如图所示，AB是⊙O的直径，G为AB延长线上的一点，GCD是⊙O的割线，过点G作 AB的垂线，交AC的延长线于点 E，交AD的延长线于点F，过G作⊙O的切线，切点为H，求证：（1）C，D，F，E四点共圆；
（2）GH2=GE•GF．
考点：与圆有关的比例线段,圆內接多边形的性质与判定
专题：立体几何
分析：（1）连接BC，由已知得∠ACB=90°，∠AGE=90°，∠FDC+∠CEF=180°，由此能证明C，D，F，E四点共圆．
（2）由切割线定理得GH2=GC•GD，由C，D，F，E四点共圆，得△GCE∽△GFD，由此能证明CH2=GE•GF．
（2）由切割线定理得GH2=GC•GD，由C，D，F，E四点共圆，得△GCE∽△GFD，由此能证明CH2=GE•GF．
解答：
选修4-1：几何证明选讲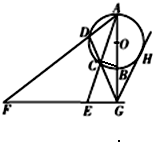
证明：（1）连接BC．
∵AB是⊙O的直径，∴∠ACB=90°．…1分
∵AG⊥FG，∴∠AGE=90°．
又∠EAG=∠BAC，∴∠ABC=∠AEG．…2分
又∠FDC=∠ABC，∴∠FDC=∠AEG．…3分
∴∠FDC+∠CEF=180°．…4分
∴C，D，F，E四点共圆．…5分
（2）∵GH为⊙O的切线，GCD为割线，
∴GH2=GC•GD．…6分
由C，D，F，E四点共圆，
得∠GCE=∠AFE，∠GEC=∠GDF．
∴△GCE∽△GFD．…7分
∴
=
，即GC•GD=GE•GF，…8分
∴CH2=GE•GF．…10分．
证明：（1）连接BC．
∵AB是⊙O的直径，∴∠ACB=90°．…1分
∵AG⊥FG，∴∠AGE=90°．
又∠EAG=∠BAC，∴∠ABC=∠AEG．…2分
又∠FDC=∠ABC，∴∠FDC=∠AEG．…3分
∴∠FDC+∠CEF=180°．…4分
∴C，D，F，E四点共圆．…5分
（2）∵GH为⊙O的切线，GCD为割线，
∴GH2=GC•GD．…6分
由C，D，F，E四点共圆，
得∠GCE=∠AFE，∠GEC=∠GDF．
∴△GCE∽△GFD．…7分
∴
| GC |
| GE |
| GF |
| GD |
∴CH2=GE•GF．…10分．
点评：本题考查四点共圆的证明，考查等式相等的证明，是中档题，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
复数-
的共轭复数是（ ）
| 1+i |
| i |
| A、1-i | B、-1+i |
| C、1+i | D、-1-i |
设全集U={1，2，3，4，5，6，7，8}，A={1，2，3}，B={3，4，5，6}，则A∩（∁UB）=（ ）
| A、{1，2，3} |
| B、{1，2} |
| C、{1，3} |
| D、{1} |
过抛物线y2=4x（p＞0）的焦点作两条互相垂直的弦AB、CD，则
+
=（ ）
| 1 |
| |AB| |
| 1 |
| |CD| |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
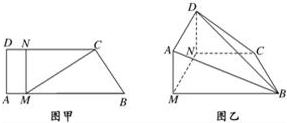如图甲，直角梯形ABCD中，AB∥CD，∠ADC=90°，点M，N分别在线段AB、CD上，且MN⊥AB，BC=1，MB=2，∠CBM=60°，若梯形ABCD沿MN折起，使DN⊥NC，如图乙．
由正整点坐标（横坐标和纵坐标都是正整数）表示的一组平面向量