题目内容
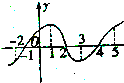 如图所示的是函数y=f(x)的导函数y=f′(x)的图象,则[-2,5]上函数f(x)的递增区间为
如图所示的是函数y=f(x)的导函数y=f′(x)的图象,则[-2,5]上函数f(x)的递增区间为考点:函数的单调性与导数的关系
专题:导数的概念及应用
分析:由导函数y=f′(x)的图象求出f′(x)≥0对应的区间,由导数与函数的单调性关系求出增区间.
解答:
解:由导函数y=f′(x)的图象得,
当x∈[-1,2]和[4,5]时,f′(x)≥0,
所以在[-2,5]上函数f(x)的递增区间为:[-1,2]和[4,5],
故答案为:[-1,2]和[4,5].
当x∈[-1,2]和[4,5]时,f′(x)≥0,
所以在[-2,5]上函数f(x)的递增区间为:[-1,2]和[4,5],
故答案为:[-1,2]和[4,5].
点评:本题考查导数与函数的单调性关系,以及识图能力,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
阅读如图所示的程序框图,运行相应的程序,若输出的结果是24,则判断框中应填入的内容为( )


| A、n≤3? | B、n≤4? |
| C、n≤5? | D、n≤6? |
过抛物线y2=4x(p>0)的焦点作两条互相垂直的弦AB、CD,则
+
=( )
| 1 |
| |AB| |
| 1 |
| |CD| |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
 由正整点坐标(横坐标和纵坐标都是正整数)表示的一组平面向量
由正整点坐标(横坐标和纵坐标都是正整数)表示的一组平面向量| ai |
| am |
| am |
|
| a1 |
| a2 |
| a3 |
| a4 |
| a2015 |
| A、(44,11) |
| B、(44,10) |
| C、(45,11) |
| D、(45,10) |
已知底面边长为2cm,侧棱长为2
cm的正四棱柱各顶点都在同一球面上,则该球的体积为( )
| 3 |
A、
| ||||
B、5
| ||||
C、
| ||||
D、5
|