题目内容
在△ABC中,a2+b2-ab=c2=
S△ABC,试确定△ABC的形状.
4
| ||
| 3 |
考点:余弦定理,正弦定理
专题:解三角形
分析:由题意得a2+b2-ab=c2,利用余弦定理和内角的范围求出C,再由题意和三角形的面积公式化简c2=
S△ABC,得到边之间的关系,即可判断三角形的形状.
4
| ||
| 3 |
解答:
解:由题意得,a2+b2-ab=c2,则a2+b2-c2=ab,①
由余弦定理得,cosC=
=
,
因为0<C<π,所以C=
,
因为c2=
S△ABC,所以c2=
×
absin
,
则以c2=
×
ab×
,即c2=ab,
代入①得,a2+b2-ab=ab,则(a-b)2=0,即a=b,
又C=
,所以△ABC是等边三角形.
由余弦定理得,cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
因为0<C<π,所以C=
| π |
| 3 |
因为c2=
4
| ||
| 3 |
4
| ||
| 3 |
| 1 |
| 2 |
| π |
| 3 |
则以c2=
4
| ||
| 3 |
| 1 |
| 2 |
| ||
| 2 |
代入①得,a2+b2-ab=ab,则(a-b)2=0,即a=b,
又C=
| π |
| 3 |
点评:本题考查余弦定理,三角形的面积公式,内角的范围,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设全集U={1,2,3,4,5,6,7,8},A={1,2,3},B={3,4,5,6},则A∩(∁UB)=( )
| A、{1,2,3} |
| B、{1,2} |
| C、{1,3} |
| D、{1} |
 由正整点坐标(横坐标和纵坐标都是正整数)表示的一组平面向量
由正整点坐标(横坐标和纵坐标都是正整数)表示的一组平面向量| ai |
| am |
| am |
|
| a1 |
| a2 |
| a3 |
| a4 |
| a2015 |
| A、(44,11) |
| B、(44,10) |
| C、(45,11) |
| D、(45,10) |
已知{an}是各项均为正数的等比数列,且a1a2013=4,则由bn=log2an,所得数列{bn}的前2013项和为( )
| A、1 | ||
| B、2 | ||
C、
| ||
| D、2013 |
如果-1,a,b,c,-4成等比数列,那么( )
| A、b=2,ac=4 |
| B、b=2,ac=-4 |
| C、b=-2,ac=4 |
| D、b=-2,ac=-4 |
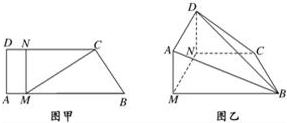 如图甲,直角梯形ABCD中,AB∥CD,∠ADC=90°,点M,N分别在线段AB、CD上,且MN⊥AB,BC=1,MB=2,∠CBM=60°,若梯形ABCD沿MN折起,使DN⊥NC,如图乙.
如图甲,直角梯形ABCD中,AB∥CD,∠ADC=90°,点M,N分别在线段AB、CD上,且MN⊥AB,BC=1,MB=2,∠CBM=60°,若梯形ABCD沿MN折起,使DN⊥NC,如图乙.