题目内容
16.计算:(Ⅰ)(-$\frac{27}{8}$)${\;}^{-\frac{2}{3}}$+${(0.002)^{-\frac{1}{2}}}$-10($\sqrt{5}$-2)-1+($\sqrt{2}$-$\sqrt{3}$)0
(Ⅱ)$\frac{1}{2}$lg$\frac{32}{49}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{245}$.
分析 (1)利用指数的运算性质即可得出.
(2)利用对数的运算性质即可得出.
解答 解:(Ⅰ)原式=$(\frac{3}{2})^{3×(-\frac{2}{3})}$+$50{0}^{-1×(-\frac{1}{2})}$-$\frac{10(\sqrt{5}+2)}{(\sqrt{5}-2)(\sqrt{5}+2)}$+1=$\frac{4}{9}$+10$\sqrt{5}$-10$\sqrt{5}$-20+1=-$\frac{167}{9}$
(Ⅱ)原式=$lg\frac{\frac{4\sqrt{2}}{7}×\sqrt{245}}{{2}^{2}}$=lg$\sqrt{10}$=$\frac{1}{2}$.
点评 本题考查了指数与对数的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
11.方程4x-2x-1+a=0有负根,则a的取值范围是( )
| A. | $a≥\frac{1}{8}$ | B. | $0<a≤\frac{1}{16}$ | C. | $-\frac{1}{8}≤a<0$ | D. | $-\frac{1}{2}<a≤\frac{1}{16}$ |
8.若函数f(x)=$\left\{\begin{array}{l}{{e}^{x}+1,x<1}\\{f(lnx),x≥1}\end{array}\right.$,则f(e)=( )
| A. | 0 | B. | 1 | C. | 2 | D. | e+1 |
6.下列四个函数中,既是奇函数又在定义域上单调递减的是( )
| A. | y=2-|x| | B. | y=tanx | C. | y=-x3 | D. | $y={log_{\frac{1}{5}}}x$ |
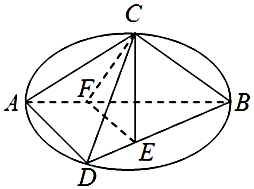 如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.
如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.