题目内容
15．已知：函数f（x）=$\sqrt{4-x}$+lg（3x-9）的定义域为集合A，集合B={x|（x-a）[x-（a+3）]＜0}，（1）若A⊆B，求实数a的取值范围；
（2）若A∩B=∅，求实数a的取值范围．
分析 （1）求出f（x）的定义域确定出A，表示出B中不等式的解集，根据A为B的子集，确定出a的范围即可；
（2）由A与B的交集为空集，确定出a的范围即可．
解答 解：（1）由函数f（x）=$\sqrt{4-x}$+lg（3x-9），得到$\left\{\begin{array}{l}{4-x≥0}\\{{3}^{x}-9＞0}\end{array}\right.$，
解得：2＜x≤4，即A=（2，4]，
由题意得：B=（a，a+3），
∵A⊆B，
∴a的范围1＜a≤2；
（2）∵A∩B=∅，
∴a+3≤2或a≥4，
解得：a≤-1或a≥4．
点评 此题考查了交集及其运算，以及集合的包含关系判断及应用，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
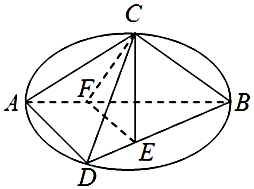如图C，D是以AB为直径的圆上的两点，AB=2AD=2$\sqrt{3}$，AC=BC，F是AB上的一点，且AF=$\frac{1}{3}$AB，CE⊥面ABD，CE=$\sqrt{2}$．