题目内容
若函数f(x)=mx2+lnx在定义域内是增函数,则实数m的取值范围是 .
考点:二次函数的性质
专题:计算题,导数的概念及应用
分析:求出f′(x)=2mx+
,x>0,因为函数在定义域内是增函数,即要说明f′(x)大于等于0,分离参数求最值,即可得到m的范围.
| 1 |
| x |
解答:
解:求导函数,可得f′(x)=2mx+
,x>0,
因为函数f(x)=mx2+lnx在定义域内是增函数,所以f′(x)≥0成立,
所以2mx+
≥0,x>0时恒成立,
所以2m≥-
,
所以2m≥0,
所以m≥0时,函数f(x)在定义域内是增函数.
故答案为:m≥0.
| 1 |
| x |
因为函数f(x)=mx2+lnx在定义域内是增函数,所以f′(x)≥0成立,
所以2mx+
| 1 |
| x |
所以2m≥-
| 1 |
| x2 |
所以2m≥0,
所以m≥0时,函数f(x)在定义域内是增函数.
故答案为:m≥0.
点评:考查学生利用导数研究函数单调性的能力,会找函数单调时自变量的取值范围,属于基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
把复数z的共轭复数记为
,已知(1+2i)
=4+3i,则z等于( )
. |
| z |
. |
| z |
| A、1+2i | B、1-2i |
| C、2-i | D、2+i |
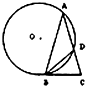 如图,△ABC中AB=AC,∠ABC=72°,圆O过A,B且与BC切于B点,与AC交于D点,连BD.若BC=2,则AC=
如图,△ABC中AB=AC,∠ABC=72°,圆O过A,B且与BC切于B点,与AC交于D点,连BD.若BC=2,则AC= 一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个三棱锥的表面积为
一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个三棱锥的表面积为