题目内容
方程
+
=1表示曲线C，给出下列四个命题，其中正确的命题个数是（ ）
①若曲线C为椭圆，则1＜t＜4
②若曲线C为双曲线，则t＜1或t＞4
③曲线C不可能是圆
④若曲线C表示焦点在X轴上的椭圆，则1＜t＜
．
| x2 |
| 4-t |
| y2 |
| t-1 |
①若曲线C为椭圆，则1＜t＜4
②若曲线C为双曲线，则t＜1或t＞4
③曲线C不可能是圆
④若曲线C表示焦点在X轴上的椭圆，则1＜t＜
| 5 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点：轨迹方程,椭圆的简单性质,双曲线的标准方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：利用椭圆、双曲线的定义，结合标准方程，即可得出结论．
解答：
解：由4-t=t-1，可得t=
，方程
+
=1表示圆，故①③不正确；
由双曲线的定义可知：当（4-t）（t-1）＜0时，即t＜1或t＞4时方程
+
=1表示双曲线，故③正确；
由椭圆定义可知：当椭圆在x轴上时，满足4-t＞t-1＞0，即1＜t＜
时方程
+
=1表示焦点在x轴上的椭圆，故④正确．
故选：B．
| 5 |
| 2 |
| x2 |
| 4-t |
| y2 |
| t-1 |
由双曲线的定义可知：当（4-t）（t-1）＜0时，即t＜1或t＞4时方程
| x2 |
| 4-t |
| y2 |
| t-1 |
由椭圆定义可知：当椭圆在x轴上时，满足4-t＞t-1＞0，即1＜t＜
| 5 |
| 2 |
| x2 |
| 4-t |
| y2 |
| t-1 |
故选：B．
点评：本题考查了圆锥曲线的标准方程，尤其要注意椭圆在x轴和y轴上两种情况，属于基础题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
把二进制的数101111（2）化成十进制的数是（ ）
| A、47 | B、56 | C、122 | D、64 |
已知
、
为非零不共线向量，向量8
-k
与-k
+
共线，则k=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||
B、-2
| ||
C、±2
| ||
| D、8 |
角θ的终边经过点P（2，-1），则sinθ=（ ）
| A、2 | ||||
| B、-1 | ||||
C、
| ||||
D、-
|
已知a＞b＞0，c∈R，则下列不等式恒成立的是（ ）
| A、ac＞bc | ||||
| B、c-a＞c-b | ||||
| C、a2＜b2 | ||||
D、
|
抛掷3个骰子，当至少一个5点或一个6点出现时，就说这次试验成功，则在54次试验中成功次数n的期望为（ ）
| A、19 | B、27 | C、54 | D、38 |
如图，在四棱锥P-ABCD中，底面ABCD是菱形，PA=PB，且侧面PAB⊥平面ABCD，点E是棱AB的中点．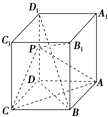
如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P为DD1的中点．求证：