题目内容
在等差数列{an}中,已知a4=10,且a3,a6,a10成等比数列.
(1)求an;
(2)设bn=2 an(n∈N*),求数列{bn}的前n项和Sn.
(1)求an;
(2)设bn=2 an(n∈N*),求数列{bn}的前n项和Sn.
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)设出等差数列{an}的公差为d,又a4=10,把a3,a6,a10用d表示,结合a3,a6,a10成等比数列求得d,则等差数列的通项公式可求;
(2)把(1)中求得的an代入bn=2 an(n∈N*),然后利用等比数列的前n项和公式求得数列{bn}的前n项和Sn.
(2)把(1)中求得的an代入bn=2 an(n∈N*),然后利用等比数列的前n项和公式求得数列{bn}的前n项和Sn.
解答:
解:(1)设等差数列{an}的公差为d,又a4=10,
可得a3=10-d,a6=10+2d,a10=10+6d,
由a3,a6,a10成等比数列,得(10+2d)2=(10-d)(10+6d),解得d=0或d=1.
若d=0,则a1=an=10,
若d=1,则a1=a4-3d=10-3×1=7,an=a1+(n-1)d=n+6.
故an=10或an=n+6;
(2)由bn=2 an(n∈N*),
若an=10,则bn=210=1024,故Sn=1024n;
若an=n+6;则bn=2n+6,
∵
=
=2,∴数列{bn}是首项为b1=27=128,公比为2的等比数列,
故Sn=
=2n+7-128.
可得a3=10-d,a6=10+2d,a10=10+6d,
由a3,a6,a10成等比数列,得(10+2d)2=(10-d)(10+6d),解得d=0或d=1.
若d=0,则a1=an=10,
若d=1,则a1=a4-3d=10-3×1=7,an=a1+(n-1)d=n+6.
故an=10或an=n+6;
(2)由bn=2 an(n∈N*),
若an=10,则bn=210=1024,故Sn=1024n;
若an=n+6;则bn=2n+6,
∵
| bn+1 |
| bn |
| 2n+7 |
| 2n+6 |
故Sn=
| 128(1-2n) |
| 1-2 |
点评:本题考查了等差数列的通项公式,考查了等比数列的性质,考查了等比数列的前n项和,是中档题.

练习册系列答案
相关题目
在平行四边形ABCD中,AC为一条对角线,
=(2,4),
=(1,3),则
等于( )
| AB |
| AC |
| BD |
| A、(2,4) |
| B、(3,5) |
| C、(-3,-5) |
| D、(-2,-4) |
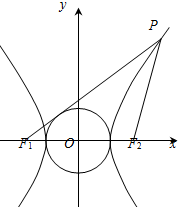 已知双曲线
已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=sin(x+φ)在区间(
,
)上单调递增,常数φ的值可能是( )
| π |
| 3 |
| 2π |
| 3 |
| A、0 | ||
B、
| ||
| C、π | ||
D、
|
若实数x,y满足
,则z=(
)2x+y的最小值为( )
|
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
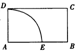 如图,四边形ABCD为矩形,AB=
如图,四边形ABCD为矩形,AB=