题目内容
4.已知两圆相交于A(-1,3),B(-6,m)两点,且这两圆的圆心均在直线x-y+c=0上,则m+2c的值为( )| A. | -1 | B. | 26 | C. | 3 | D. | 2 |
分析 由圆的性质可知,AB与x-y+c=0垂直且AB被x-y+c=0平分,可求KAB,从而可求m,然后由AB的中点在直线上可求c,结合选项可判断.
解答 解:由圆的性质可知,AB与x-y+c=0垂直且AB被x-y+c=0平分,
∴KAB=$\frac{m-3}{-6+1}$=-1,
∴m=8,
∵AB的中点在直线上,
∴AB的中点(-$\frac{7}{2}$,$\frac{11}{2}$)代入方程得c=9,
∴m+2c=8+18=26.
故选:B.
点评 本题主要考查了两圆相交性质:两圆的公共弦被连心线垂直平分的应用,属于基础试题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
15.已知全集U={1,2,3,4},A={1,2},则满足A⊆B的集合B个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.在复平面xOy内,若A(2,-1),B(0,3),则?OACB中,点C对应的复数为( )
| A. | 2+2i | B. | 2-2i | C. | 1+i | D. | 1-i |
9.设函数f(x)在点x0附近有定义,且有f(x0+△x)-f(x0)=a△x+b(△x)2,其中a,b为常数,则( )
| A. | f'(x)=a | B. | f'(x)=b | C. | f'(x0)=a | D. | f'(x0)=b |
16.已知$\frac{\overline z}{1+i}=2+i$,则复数z=( )
| A. | 1-3i | B. | -1-3i | C. | -1+3i | D. | 1+3i |
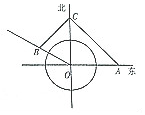 某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路,工厂正北方向有一观察站C,OC=2千米,因化工厂原料泄漏,工厂周围1千米的范围内均有不同程度的影响.现准备从观察站C处修两条隔离绿化带CA,CB(其中A,B为隔离带与公路交接点).且使CA⊥CB,隔离带与两条公路线围成的面积为S.
某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路,工厂正北方向有一观察站C,OC=2千米,因化工厂原料泄漏,工厂周围1千米的范围内均有不同程度的影响.现准备从观察站C处修两条隔离绿化带CA,CB(其中A,B为隔离带与公路交接点).且使CA⊥CB,隔离带与两条公路线围成的面积为S.