题目内容
已知m为常数,函数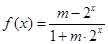 为奇函数.
为奇函数.
(1)求m的值;
(2)若 ,试判断
,试判断 的单调性(不需证明);
的单调性(不需证明);
(3)若 ,存在
,存在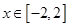 ,使
,使 ,求实数k的最大值.
,求实数k的最大值.
(1) ;(2)在R上单调递增;(3)
;(2)在R上单调递增;(3) .
.
解析试题分析: (1)由奇函数的定义得: ,将解析式代入化简便可得m的值;
,将解析式代入化简便可得m的值;
(2) ,结合指数函数与反比例函数的单调性,便可判定
,结合指数函数与反比例函数的单调性,便可判定 的单调性;
的单调性;
(3)对不等式: ,不宜代入解析式来化简,而应将进行如下变形:
,不宜代入解析式来化简,而应将进行如下变形: ,然后利用单调性去掉
,然后利用单调性去掉 ,从而转化为:
,从而转化为: .
.
进而变为: .由题设知:
.由题设知: .这样只需求出
.这样只需求出 的最大值即可. 而
的最大值即可. 而 ,所以
,所以 在[-2,2]上单调递增,
在[-2,2]上单调递增,
所以 .
.
试题解析:(1)由 ,得
,得 ,
,
∴ ,即
,即 ,
,
∴ . ..4分
. ..4分
(2) ,在R上单调递增. 7分
,在R上单调递增. 7分
(3)由 得
得 ,9分
,9分
即 .
.
令 ,则
,则 ,
,
所以 在[-2,2]上单调递增,
在[-2,2]上单调递增,
所以 ,
,
所以 ,从而
,从而 .12分
.12分
考点:1、函数的奇偶性和单调性;2、不等关系.

练习册系列答案
相关题目
 ,恒过定点
,恒过定点 .
. ;
; 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 ,设函数
,设函数 ,直接写出
,直接写出 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
. 恒成立,求
恒成立,求 的最大值;
的最大值; 为常数,且
为常数,且 ,记
,记 ,求
,求 的最小值.
的最小值. 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域; .
. 时,证明:函数
时,证明:函数 不是奇函数;
不是奇函数; 与
与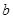 的值;
的值; 的解集.
的解集. 是奇函数
是奇函数 上单调递增,求实数a的取值范围
上单调递增,求实数a的取值范围 为偶函数.
为偶函数.  的值;
的值; 有且只有一个根, 求实数
有且只有一个根, 求实数 的取值范围.
的取值范围. 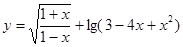 的定义域为
的定义域为 ,
, 时,求
时,求 的最小值.
的最小值.

 .
. 的单调区间;
的单调区间; ,对
,对 都有
都有 成立,求实数
成立,求实数 的取值范围;
的取值范围; (
( 且
且 ).
).