题目内容
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
(Ⅰ)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的 .
.
(Ⅰ) ;(Ⅱ)当
;(Ⅱ)当 时,建造费用最小时
时,建造费用最小时 当
当 时,建造费用最小时
时,建造费用最小时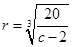 .
.
解析试题分析:(Ⅰ)由圆柱和球的体积的表达式,得到l和r的关系.再由圆柱和球的表面积公式建立关系式,将表达式中的l用r表示.并注意到写定义域时,利用l≥2r,求出自变量r的范围;(Ⅱ)用导数的知识解决,注意到定义域的限制,在区间(0,2]中,极值未必存在,将极值点在区间内和在区间外进行分类讨论.
试题解析:(I)设容器的容积为V,由题意知
故
由于 因此
因此 .3分
.3分
所以建造费用
因此 ..5分
..5分
(II)由(I)得
由于 当
当
令
 ;所以
;所以 .7分
.7分
(1)当 时,
时,
所以 是函数y的极小值点,也是最小值点。 .10分
是函数y的极小值点,也是最小值点。 .10分
(2)当 即
即 时, 当
时, 当 函数单调递减,
函数单调递减,
所以r=2是函数y的最小值点,
综上所述,当 时,建造费用最小时
时,建造费用最小时
当 时,建造费用最小时
时,建造费用最小时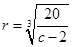 13分
13分
考点:1.函数解析式和定义域;2.函数模型的应用;3.函数最值的求法

练习册系列答案
相关题目
 与
与 交于
交于 两点且
两点且 ,奇函数
,奇函数 ,当
,当 时,
时, 与
与 都在
都在 取到最小值.
取到最小值. 的解析式;
的解析式; 图象恰有两个不同的交点,求实数
图象恰有两个不同的交点,求实数 的取值范围.
的取值范围. .
. 的定义域为A,求集合A;
的定义域为A,求集合A; )上单调性,并用单调性的定义加以证明.
)上单调性,并用单调性的定义加以证明. 的定义域为
的定义域为 ,并且满足
,并且满足 ,且
,且 ,当
,当 时,
时,
 的值;(3分)
的值;(3分) 的奇偶性;(3分)
的奇偶性;(3分) ,求
,求 的取值范围.(6分)
的取值范围.(6分) 来拟合该景点对外开放的第
来拟合该景点对外开放的第
 年与当年的游客人数
年与当年的游客人数 (单位:万人)之间的关系.
(单位:万人)之间的关系. =
= ,试确定
,试确定 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测; ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定 的取值范围.
的取值范围. 为奇函数,且当
为奇函数,且当 时,
时, .当
.当 时,
时, ,最小值为
,最小值为 ,求
,求 的值.
的值.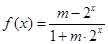 为奇函数.
为奇函数. ,试判断
,试判断 的单调性(不需证明);
的单调性(不需证明);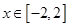 ,使
,使 ,求实数k的最大值.
,求实数k的最大值. 的函数
的函数 (
( 为实数)。
为实数)。 是奇函数,求
是奇函数,求 都有
都有 成立.
成立. ,
, 
 .
. , 函数
, 函数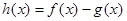 在其定义域是增函数,求
在其定义域是增函数,求 的取值范围;
的取值范围;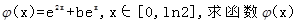 的最小值;
的最小值; 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 ,过线段
,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 ,问是否存在点
,问是否存在点