题目内容
已知 .
.
(1)若 恒成立,求
恒成立,求 的最大值;
的最大值;
(2)若 为常数,且
为常数,且 ,记
,记 ,求
,求 的最小值.
的最小值.
(1)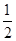 ;(2)
;(2)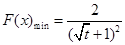 .
.
解析试题分析:本题考查导数与函数及运用导数求单调区间、最值等数学知识,突出考查运用数学知识和方法分析问题解决问题的能力.第一问,是恒成立问题,先将恒成立问题转化为最值问题,求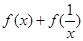 的最值是本问的关键,法一,利用基本不等式求最值,法二,利用导数求最值,无论用哪种方法都应注意函数的定义域;第二问,令
的最值是本问的关键,法一,利用基本不等式求最值,法二,利用导数求最值,无论用哪种方法都应注意函数的定义域;第二问,令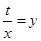 ,将
,将 进行转化,化简成
进行转化,化简成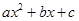 的形式,利用二次函数的单调性求
的形式,利用二次函数的单调性求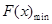 .
.
试题解析:(1)(解法一)
设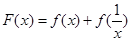
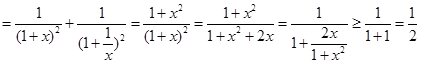 ,
,
∴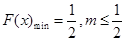 ,∴
,∴ 的最大值为
的最大值为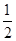 .
.
(解法二)设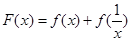
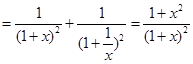 ,
,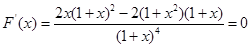 ,
,
∴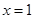 ,当
,当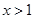 时,
时,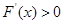 ,当
,当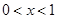 时,
时,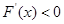 ,∴
,∴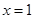 为极小值点,
为极小值点,
∴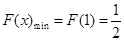 ,∴
,∴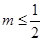 ,∴
,∴ 的最大值为
的最大值为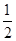 .
.
(2)设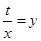 ,则
,则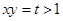 ,则
,则
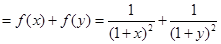
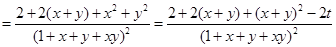
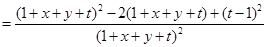
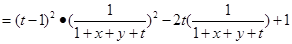
令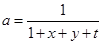 ,则
,则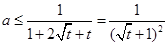
即 ,
,
设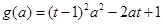 ,∵
,∵ 其对称轴
其对称轴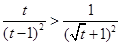 ,
, 在
在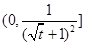 上单调递减,∴
上单调递减,∴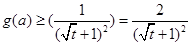 ,
,
∴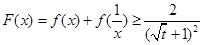 ,
,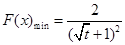 .
.
考点:1.恒成立问题;2.基本不等式;3.利用导数求函数的单调区间和最值;4.二次函数的单调性和最值.

练习册系列答案
相关题目
 .
. 为奇函数,求实数
为奇函数,求实数 的值;
的值; ,都有
,都有 成立,求实数
成立,求实数 。
。 的定义域;
的定义域; 的值,作出函数
的值,作出函数 的图象并指出函数
的图象并指出函数 .
. 的定义域为A,求集合A;
的定义域为A,求集合A; )上单调性,并用单调性的定义加以证明.
)上单调性,并用单调性的定义加以证明. ,当
,当 时,对应
时,对应 值的集合为
值的集合为 .
. 的值;(2)若
的值;(2)若 ,求该函数的最值.
,求该函数的最值. 的定义域为
的定义域为 ,并且满足
,并且满足 ,且
,且 ,当
,当 时,
时,
 的值;(3分)
的值;(3分) 的奇偶性;(3分)
的奇偶性;(3分) ,求
,求 的取值范围.(6分)
的取值范围.(6分) 来拟合该景点对外开放的第
来拟合该景点对外开放的第
 年与当年的游客人数
年与当年的游客人数 (单位:万人)之间的关系.
(单位:万人)之间的关系. =
= ,试确定
,试确定 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测; ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定 的取值范围.
的取值范围. 为奇函数.
为奇函数. ,试判断
,试判断 的单调性(不需证明);
的单调性(不需证明); ,使
,使 ,求实数k的最大值.
,求实数k的最大值. .
. ,解不等式
,解不等式 ;
; ,
, ,求实数
,求实数 的取值范围.
的取值范围.