题目内容
14.一圆锥的侧面积是其底面积的2倍,若圆锥的高为$\sqrt{3}$,则其表面积为( )| A. | $\frac{3\sqrt{3}π}{2}$ | B. | 6π | C. | 3π | D. | 3$\sqrt{3}$π |
分析 设底面半径为r,根据条件列出方程求出r,代入面积公式求出.
解答 解:设圆锥底面半径为r,则圆锥的母线l=$\sqrt{{r}^{2}+3}$,
∴S侧面=πr$\sqrt{{r}^{2}+3}$=2πr2,解得r=1,
∴S表=3S底面=3π×12=3π.
故选:C.
点评 本题考查了圆锥的结构特征,面积计算,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
5.如果直线3ax+y-1=0与直线(1-2a)x+ay+1=0平行.那么a等于( )
| A. | -1 | B. | $\frac{1}{3}$ | C. | 3 | D. | -1或$\frac{1}{3}$ |
2.函数f(x)=x2-($\frac{1}{2}$)|x|的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
3.执行如图所示的程序框图,输出的结果是( )
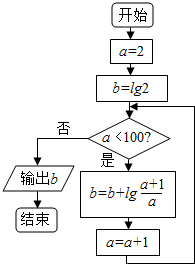

| A. | lg97 | B. | lg98 | C. | lg99 | D. | 2 |
4.已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2015)=3,则f(2016)的值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | 3 |