题目内容
15.已知复数z=x+yi(x、y∈R).(1)z满足|z-4i|=|z+2|,求2x+4y的最小值及相应x、y值.
(2)z满足|z-1|+|z+1|=4.求|z|的取值范围.
分析 (1)由复数模长的几何意义和线段的垂直平分线可得x+2y=3,由基本不等式可得;
(2)由复数模长的几何意义$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,三角换元可得x=2cosθ,y=$\sqrt{3}$sinθ,由复数的模长公式和三角函数可得.
解答 解:(1)∵z满足|z-4i|=|z+2|,
∴z=x+yi表示到(0,4)和(-2,0)距离相等的点,
由线段的垂直平分线可得x+2y=3,
故2x+4y≥2$\sqrt{{2}^{x}•{4}^{y}}$=2$\sqrt{{2}^{x+2y}}$=4$\sqrt{2}$,
当且仅当2x=4y即x=$\frac{3}{2}$且y=$\frac{3}{4}$时取等号
故2x+4y的最小值为4$\sqrt{2}$,相应x、y值分别为$\frac{3}{2}$和$\frac{3}{4}$;
(2)∵z满足|z-1|+|z+1|=4.
∴z在以(-1,0)和(1,0)为焦点的椭圆上
可得椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
故可得x=2cosθ,y=$\sqrt{3}$sinθ
∴|z|2=4cos2θ+3sin2θ=3+cos2θ∈[3,4],
∴|z|的取值范围为[$\sqrt{3}$,2]
点评 本题考查复数求模,涉及基本不等式和三角换元的思想,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.如果直线3ax+y-1=0与直线(1-2a)x+ay+1=0平行.那么a等于( )
| A. | -1 | B. | $\frac{1}{3}$ | C. | 3 | D. | -1或$\frac{1}{3}$ |
3.执行如图所示的程序框图,输出的结果是( )
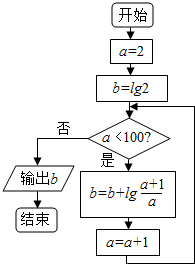

| A. | lg97 | B. | lg98 | C. | lg99 | D. | 2 |
10.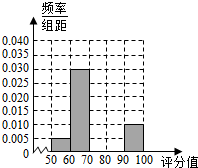 某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
(2)将成绩按分层抽样的方法抽取150名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率.
 某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
| 成绩分组 | 频数 | 频率 |
| [50,60] | 100 | |
| (60,70] | ||
| (70,80] | 800 | |
| (80,90] | ||
| (90,100] | 200 |
20.在复平面上作出满足下列条件的复数在复平面上对应的点集所表示的图形.
(1)|z|<2;(2)1≤|z|<3;(3)Rez=2;
(4)1<Rez<2且1<lmz<2;(5)|z|>3且lmz<-1.
(1)|z|<2;(2)1≤|z|<3;(3)Rez=2;
(4)1<Rez<2且1<lmz<2;(5)|z|>3且lmz<-1.
4.已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2015)=3,则f(2016)的值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | 3 |