题目内容
20.设$\overrightarrow a=({3,2}),\overrightarrow b=({-1,k})$,若$\overrightarrow{a}$与2$\overrightarrow{a}$+$\overrightarrow{b}$共线,则k=-$\frac{2}{3}$.分析 由题意和向量共线可得a的方程,解方程可得.
解答 解:∵$\overrightarrow a=({3,2}),\overrightarrow b=({-1,k})$,
∴2$\overrightarrow{a}$+$\overrightarrow{b}$=(5,4+k),
∵$\overrightarrow{a}$与2$\overrightarrow{a}$+$\overrightarrow{b}$共线,
∴3(4+k)-2×5=0,
解得k=-$\frac{2}{3}$
故答案为:-$\frac{2}{3}$
点评 本题考查平行向量与共线向量,属基础题.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.抛物线y2=2px(p>0)的焦点为F,过原点O作直线l:y=kx,与抛物线的另一交点为点A,过A作l的垂线交x轴于点B,则下列命题中正确的是( )
| A. | 存在无数个实数k使得点F为线段OB的中点 | |
| B. | 存在唯一的实数k使得点F为线段OB的中点 | |
| C. | 不存在实数k使得点F为线段OB的中点 | |
| D. | 以上命题都不正确 |
15.已知集合A={x|log2(x-4)≤0},B={y|y=ax+1(a>0且a≠1)},则(∁RA)∩B=( )
| A. | (5,+∞) | B. | (1,4]∪(5,+∞) | C. | [1,4)∪[5,+∞) | D. | [1,4) |
5.如果直线3ax+y-1=0与直线(1-2a)x+ay+1=0平行.那么a等于( )
| A. | -1 | B. | $\frac{1}{3}$ | C. | 3 | D. | -1或$\frac{1}{3}$ |
10.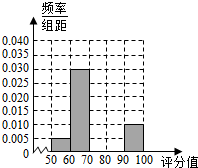 某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
(2)将成绩按分层抽样的方法抽取150名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率.
 某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
| 成绩分组 | 频数 | 频率 |
| [50,60] | 100 | |
| (60,70] | ||
| (70,80] | 800 | |
| (80,90] | ||
| (90,100] | 200 |