题目内容
13.已知α是第二象限角,且3sinα+4cosα=0,则tan$\frac{α}{2}$=( )| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
分析 由已知利用同角三角函数基本关系式可求tanα的值,利用二倍角的正切函数公式可得:2tan2$\frac{α}{2}$-3tan$\frac{α}{2}$-2=0,结合$\frac{α}{2}$的范围,即可得解tan$\frac{α}{2}$的值.
解答 解:∵3sinα+4cosα=0,
∴3tanα+4=0,可得:tanα=-$\frac{4}{3}$=$\frac{2tan\frac{α}{2}}{1-ta{n}^{2}\frac{α}{2}}$,整理可得:2tan2$\frac{α}{2}$-3tan$\frac{α}{2}$-2=0,
∴解得:tan$\frac{α}{2}$=2,或-$\frac{1}{2}$,
∵α是第二象限角,
∴kπ+$\frac{π}{4}$<$\frac{α}{2}$<kπ+$\frac{π}{2}$,k∈Z,
∴tan$\frac{α}{2}$>0,故tan$\frac{α}{2}$=2.
故选:A.
点评 本题主要考查了同角三角函数基本关系式,二倍角的正切函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
| A. | 1365石 | B. | 338石 | C. | 169石 | D. | 134石 |
1.设定义域为R的函数f(x)=$\left\{\begin{array}{l}{0}&{x=1}\\{|lg|x-1||}&{x≠1}\end{array}\right.$,则关于x的方程f2(x)+bf(x)+c=0有7个不同实数解的充要条件是( )
| A. | b<0且c>0 | B. | b>0且c<0 | C. | b<0且c=0 | D. | b>0且c=0 |
8.已知函数f(x)=x2-ax($\frac{1}{e}$≤x≤e,e为自然对数的底数)与g(x)=ex的图象上存在关于直线y=x对称的点,则实数a取值范围是( )
| A. | [1,e+$\frac{1}{e}$] | B. | [1,e-$\frac{1}{e}$] | C. | [e-$\frac{1}{e}$,e+$\frac{1}{e}$] | D. | [e-$\frac{1}{e}$,e] |
18.若两个球的体积之比为1:8,则这两个球的表面积之比为( )
| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:16 |
5.设M是△ABC边BC上的任意一点,$\overrightarrow{AN}$=$\frac{1}{3}$$\overrightarrow{NM}$,若$\overrightarrow{AN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
2.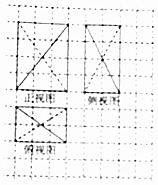 如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )| A. | 24π | B. | 29π | C. | 48π | D. | 58π |