题目内容
18.若两个球的体积之比为1:8,则这两个球的表面积之比为( )| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:16 |
分析 设这两球的半径分为r,R,由两个球的体积之比为1:8,得到r:R=1:2,由此能求出这两个球的表面积之比.
解答 解:设这两球的半径分为r,R,
∵两个球的体积之比为1:8,
∴$\frac{1}{3}π{r}^{3}:\frac{1}{3}π{R}^{3}$=r3:R3=1:8,
∴r:R=1:2,
∴这两个球的表面积之比为4πr2:4πR2=1:4.
故选:B.
点评 本题考查两个球的表面积之比的求法,是基础题,解题时要认真审题,注意球的体积公式和表面积公式的合理运用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
6.若复数z满足$\frac{\overline z}{1+i}=i$,其中i为虚数单位,则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
13.已知α是第二象限角,且3sinα+4cosα=0,则tan$\frac{α}{2}$=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
3.已知抛物线C:x2=2py(p>0),若直线y=2x,被抛物线所截弦长为4$\sqrt{5}$,则抛物线C的方程为( )
| A. | x2=8y | B. | x2=4y | C. | x2=2y | D. | x2=y |
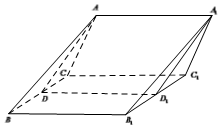 如图三棱柱ABC-A1B1C1,AB=BC=CA,D,D1分别是BC,B1C1的中点,四边形ADD1A1是菱形,且平面ADD1A1⊥平面CBB1C1.
如图三棱柱ABC-A1B1C1,AB=BC=CA,D,D1分别是BC,B1C1的中点,四边形ADD1A1是菱形,且平面ADD1A1⊥平面CBB1C1.
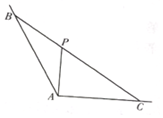 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.