题目内容
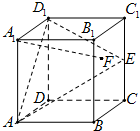 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,下列说法错误的是( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,下列说法错误的是( )| A、点F的轨迹是一条线段 |
| B、A1F与BE不在同一平面 |
| C、三棱锥F-A1D1A的体积为定值 |
| D、A1F与D1E不可能平行 |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:分别根据线面平行的性质定理以及异面直线的定义,判断A是否正确;
根据异面直线的判定定理,判断B是否正确;
利用点面距离的转化与棱锥的体积公式,判断C是否正确;
根据当F与M重合时,此时A1F∥D1E,可得D错误.
根据异面直线的判定定理,判断B是否正确;
利用点面距离的转化与棱锥的体积公式,判断C是否正确;
根据当F与M重合时,此时A1F∥D1E,可得D错误.
解答:
解:对A. 设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点
设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点
分别取B1B、B1C1的中点M、N,连接AM、MN、AN,则
∵A1M∥D1E,A1M?平面D1AE,D1E?平面D1AE,∴A1M∥平面D1AE.同理可得MN∥平面D1AE,
∵A1M、MN是平面A1MN内的相交直线,∴平面A1MN∥平面D1AE,
由此结合A1F∥平面D1AE,可得直线A1F?平面A1MN,即点F的轨迹是线段MN,∴A正确.
对B.由A知,平面A1MN∥平面D1AE,∴A1F与D1E不可能平行,∴B正确.
对C.∵F∈MN,MN?平面B1MN,平面B1MN∥平面AA1D1,∴VF-AA1D1=VB1-AA1D1,∴三棱锥F-A1D1A的体积为定值,∴C正确.
对D.当F与M重合时,∵M为BB1的中点,此时A1F∥D1E,∴D错误.
故选:D.
 设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点
设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点分别取B1B、B1C1的中点M、N,连接AM、MN、AN,则
∵A1M∥D1E,A1M?平面D1AE,D1E?平面D1AE,∴A1M∥平面D1AE.同理可得MN∥平面D1AE,
∵A1M、MN是平面A1MN内的相交直线,∴平面A1MN∥平面D1AE,
由此结合A1F∥平面D1AE,可得直线A1F?平面A1MN,即点F的轨迹是线段MN,∴A正确.
对B.由A知,平面A1MN∥平面D1AE,∴A1F与D1E不可能平行,∴B正确.
对C.∵F∈MN,MN?平面B1MN,平面B1MN∥平面AA1D1,∴VF-AA1D1=VB1-AA1D1,∴三棱锥F-A1D1A的体积为定值,∴C正确.
对D.当F与M重合时,∵M为BB1的中点,此时A1F∥D1E,∴D错误.
故选:D.
点评:本题考查了空间直线与平面平行关系的判定与性质,考查了异面直线的判定及棱锥的体积公式,综合性较强,正确的作出图形是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设数列{an}满足an=
(n∈N+),若数列{an}是递增数列,则b的范围是( )
|
| A、(0,3) | ||
B、(0,2+
| ||
| C、(1,3] | ||
D、(0,2+
|
如图所示的程序框图,若执行运算1×
×
×
×
,则在空白执行框中,应该填入( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |

| A、T=T•(i+1) | ||
| B、T=T•i | ||
C、T=T•
| ||
D、T=T•
|
等比数列{an}的首项为1,其前n项和为Sn,如果
=3,则a5的值为( )
| S4 |
| S2 |
| A、2 | B、2或-2 |
| C、4 | D、4或-4 |
下列有关命题的说法正确的是( )
A、“θ≠60°”是“cosθ≠
| ||
| B、“x=2”是“x2-5x+6=0”的必要不充分条件 | ||
| C、命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | ||
| D、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
设在各交通岗遇到红灯的事件是相互独立的,且概率都是0.4,则此人三次上班途中遇红灯的次数的期望为( )
| A、0.4 |
| B、1.2 |
| C、0.43 |
| D、0.6 |
函数f(x)=Msinωx(ω>0),在区间[a,b]上是增函数,且f(a)=-M,f(b)=M,则函数f(x)=Mcosωx在区间[a,b]上( )
| A、是增函数 |
| B、是减函数 |
| C、可以取得最大值M |
| D、可以取得最小值-M |