题目内容
已知等差数列{an}的前13项和S13=39，则a2+a4+a15=（ ）
| A、3 | B、6 | C、9 | D、12 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列的求和公式，求出a7=3，再利用等差数列的通项公式，即可求得结论．
解答：
解：∵等差数列{an}的前13项和S13=39，
∴
（a1+a13）=39，
∴a7=3，
∴a2+a4+a15=a1+d+a1+3d+a1+14d=3（a1+6d）=3a7=9．
故选：C．
∴
| 13 |
| 2 |
∴a7=3，
∴a2+a4+a15=a1+d+a1+3d+a1+14d=3（a1+6d）=3a7=9．
故选：C．
点评：本题主要考查等差数列的定义和性质，等差数列的前n项和公式的应用，属于基础题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
如图所示的程序框图，若执行运算1×
×
×
×
，则在空白执行框中，应该填入（ ）
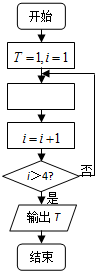
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| A、T=T•（i+1） | ||
| B、T=T•i | ||
C、T=T•
| ||
D、T=T•
|
下列有关命题的说法正确的是（ ）
A、“θ≠60°”是“cosθ≠
| ||
| B、“x=2”是“x2-5x+6=0”的必要不充分条件 | ||
| C、命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1＜0” | ||
| D、命题“若x=y，则sinx=siny”的逆否命题为真命题 |
设在各交通岗遇到红灯的事件是相互独立的，且概率都是0.4，则此人三次上班途中遇红灯的次数的期望为（ ）
| A、0.4 |
| B、1.2 |
| C、0.43 |
| D、0.6 |
已知f（x）是定义在R上的偶函数，函数周期为2，且在区间[0，1]上是增函数，则f（-5.5）、f（-1）、f（2）的大小关系是（ ）
| A、f（-5.5）＜f（2）＜f（-1） |
| B、f（-1）＜f（-5.5）＜f（2） |
| C、f（2）＜f（-5.5）＜f（-1） |
| D、f（-1）＜f（2）＜f（-5.5） |
函数f（x）=Msinωx（ω＞0），在区间[a，b]上是增函数，且f（a）=-M，f（b）=M，则函数f（x）=Mcosωx在区间[a，b]上（ ）
| A、是增函数 |
| B、是减函数 |
| C、可以取得最大值M |
| D、可以取得最小值-M |
如图所示扇形AOB，半径为2，∠AOB=