题目内容
7.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)-4cos2$\frac{ωx}{2}$+3(其中ω>0,x∈R).(Ⅰ)求函数f(x)的值域;
(Ⅱ)若函数f(x)的图象与直线y=1的相邻两交点间的距离为$\frac{π}{2}$,求函数f(x)的单调递减区间.
分析 (Ⅰ)利用三角恒等变换化简函数f(x)为正弦型函数,根据正弦函数的有界性求出f(x)的值域;
(Ⅱ)由题设条件与三角函数的图象和性质可知f(x)的周期为π,求出ω的值,再根据正弦函数的单调性求出f(x)的单调递减区间.
解答 解:(Ⅰ)函数f(x)=2sin(ωx+$\frac{π}{6}$)-4cos2$\frac{ωx}{2}$+3
=2($\frac{\sqrt{3}}{2}$sinωx+$\frac{1}{2}$cosωx)-2cosωx+1
=2($\frac{\sqrt{3}}{2}$sinωx-$\frac{1}{2}$cosωx)+1
=2sin(ωx-$\frac{π}{6}$)+1,
由-1≤sin(ωx-$\frac{π}{6}$)≤1,
得-1≤2sin(ωx-$\frac{π}{6}$)+1≤3,
∴函数f(x)的值域为[-1,3];
(Ⅱ)由题设条件与三角函数的图象和性质可知,
函数f(x)的周期为π,
即$\frac{2π}{ω}$=π,解得ω=2;
∴f(x)=2sin(2x-$\frac{π}{6}$)+1;
令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$(k∈Z),
解得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$(k∈Z);
∴函数f(x)的单调递减区间是[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$](k∈Z).
点评 本题考查了三角恒等变换以及正弦型函数的图象和性质的应用问题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知集合A={x|(x+2)(x-3)≤0,x∈Z},B={x|(|x|-2)2=1},则A∩B=( )
| A. | {-1,1} | B. | {1,3} | C. | {-1,1,3} | D. | {-3,-1,1} |
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线y2=12x的焦点重合,且双曲线的离心率等于$\sqrt{3}$,则该双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{18}$=1 | B. | $\frac{{y}^{2}}{18}$-$\frac{{x}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 |
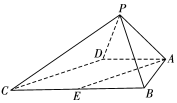 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点. 在R上是单调增函数,求实数a的取值范围。
在R上是单调增函数,求实数a的取值范围。 B的B的个数是( )
B的B的个数是( )