题目内容
15．平行四边形ABCD中，|AB|=2，|BC|=$\sqrt{2}$，∠DAB=60°，$\overrightarrow{CF}$=$\frac{1}{2}$$\overrightarrow{CB}$，$\overrightarrow{DE}$=$\frac{1}{2}\overrightarrow{EB}$，则$\overrightarrow{AE}$•$\overline{AF}$=2+$\frac{5\sqrt{2}}{6}$．分析 用$\overrightarrow{AB}，\overrightarrow{AD}$表示出$\overrightarrow{AE}，\overrightarrow{AF}$，再计算$\overrightarrow{AE}$•$\overline{AF}$．
解答 
解：${\overrightarrow{AB}}^{2}$=4，${\overrightarrow{AD}}^{2}$=2，$\overrightarrow{AB}•\overrightarrow{AD}$=2×$\sqrt{2}×cos60°$=$\sqrt{2}$，
$\overrightarrow{AE}=\overrightarrow{AD}+\frac{1}{3}\overrightarrow{DB}$=$\overrightarrow{AD}$+$\frac{1}{3}$（$\overrightarrow{AB}-\overrightarrow{AD}$）=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}\overrightarrow{AD}$，
$\overrightarrow{AF}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$，
∴$\overrightarrow{AE}•\overrightarrow{AF}$=（$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}\overrightarrow{AD}$）•（$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$）=$\frac{1}{3}$${\overrightarrow{AB}}^{2}$+$\frac{1}{3}$${\overrightarrow{AD}}^{2}$+$\frac{5}{6}$$\overrightarrow{AB}•\overrightarrow{AD}$=$\frac{4}{3}$+$\frac{2}{3}$+$\frac{5\sqrt{2}}{6}$=2+$\frac{5\sqrt{2}}{6}$．
故答案为：2+$\frac{5\sqrt{2}}{6}$．
点评 本题考查了平面向量的数量积运算，属于中档题．
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案| t | [0，15） | [15，30） | [30，45） | [45，60） | [60，75） | [75，90） |
| 男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
| 女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
（1）将频率视为概率，估计该校4000名学生中“读书迷”有多少人？
（2）从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动．
（i）求抽取的4位同学中既有男同学又有女同学的概率；
（ii）记抽取的“读书迷”中男生人数为X，求X的分布列和数学期望．
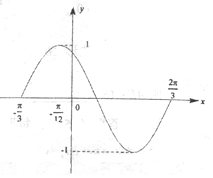如图是函数y=Asin（ωx+φ）（x∈R）在区间[-$\frac{π}{3}$，$\frac{2π}{3}$]上的图象，为了得到这个函数的图象．只需将y=cosx（x∈R）的图象上的所有点（ ）| A． | 向左平移$\frac{π}{6}$个单位长度，再把所有点的横坐标扩大到原来的2倍 | |
| B． | 向左平移$\frac{π}{12}$个单位长度．再把所有点的横坐标扩大到原来的2倍 | |
| C． | 把所有点的横坐标缩短到原来的$\frac{1}{2}$，再向左平移$\frac{π}{12}$个单位长度 | |
| D． | 把所有点的横坐标缩短到原来的$\frac{1}{2}$，再向左平移$\frac{π}{6}$个单位长度 |
，若
，则实数
的值是 ．