题目内容
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线y2=12x的焦点重合,且双曲线的离心率等于$\sqrt{3}$,则该双曲线的标准方程为( )| A. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{18}$=1 | B. | $\frac{{y}^{2}}{18}$-$\frac{{x}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 |
分析 根据题意,由抛物线的方程可得抛物线焦点坐标,即可得双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的焦点坐标,即可得c的值,再双曲线的离心率公式可得e=$\frac{c}{a}$=$\sqrt{3}$,解可得a的值,由双曲线的性质可得b的值,将a、b的值代入双曲线方程即可得答案.
解答 解:根据题意,抛物线y2=12x的焦点在x轴正半轴上,其坐标为(3,0),
则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1中,一个焦点的坐标为(3,0),即c=3,
又由双曲线的离心率e=$\sqrt{3}$,则有e=$\frac{c}{a}$=$\sqrt{3}$,解可得a=$\sqrt{3}$,
则b2=c2-a2=6,
则双曲线的标准方程为:$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1;
故选:D.
点评 本题考查双曲线、抛物线的几何性质,关键是掌握双曲线中a、b、c的关系.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
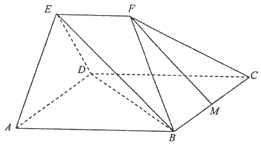 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点. ,若
,若 ,则实数
,则实数 的值是 .
的值是 .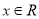 ,函数
,函数 ,
,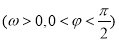 .已知
.已知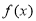 的最小正周期为
的最小正周期为 ,且
,且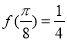 .
.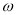 和
和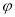 的值;
的值;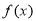 在区间
在区间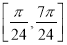 上的最小值和最大值.
上的最小值和最大值.