题目内容
18.某空间几何体的三视图如图所示,则该几何体的表面积是$32+8\sqrt{5}$.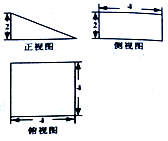
分析 由已知中的三视图可得:该几何体是一个以主视图为底面的三棱柱,代入棱柱表面积公式,可得答案.
解答 解:由已知中的三视图可得:该几何体是一个以主视图为底面的三棱柱,
底面面积为:$\frac{1}{2}$×2×4=4,
底面周长为:2+4+$\sqrt{{2}^{2}+{4}^{2}}$=6+2$\sqrt{5}$,
故棱柱的表面积S=2×4+4×(6+2$\sqrt{5}$)=$32+8\sqrt{5}$,
故答案为:$32+8\sqrt{5}$
点评 本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,简单几何体的三视图,难度基础.

练习册系列答案
相关题目
13.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦点的渐近线的距离为2,且双曲线的一条渐近线与直线x-2y+3=0平行,则双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ |
10.已知某几何体的三视图如图,则该几何体的体积是( )
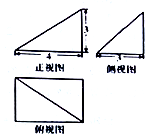

| A. | 48 | B. | 36 | C. | 24 | D. | 12 |
7.已知命题p:?x∈R,$sinx>\frac{{\sqrt{3}}}{2}$,则( )
| A. | ﹁p:?x∈R,sin $x≤\frac{{\sqrt{3}}}{2}$ | B. | ﹁p:?x∈R,$sinx<\frac{{\sqrt{3}}}{2}$ | ||
| C. | ﹁p:?x∈R | D. | ﹁p:?x∈R,$sinx≤\frac{{\sqrt{3}}}{2}$ |