题目内容
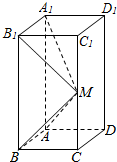 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.(Ⅰ)求异面直线A1M和C1D1所成的角的正切值;
(Ⅱ)证明:平面ABM⊥平面A1B1M.
考点:异面直线及其所成的角,平面与平面垂直的判定
专题:计算题,证明题
分析:(1)由于C1D1∥B1A1故根据异面直线所成角的定义可知∠MA1B1为异面直线A1M和C1D1所成的角然后在解三角形MA1B1求出∠MA1B1的正切值即可.
(Ⅱ)可根据题中条件计算得出A1B1⊥BM,BM⊥B1M然后再根据面面垂直的判定定理即可得证.
(Ⅱ)可根据题中条件计算得出A1B1⊥BM,BM⊥B1M然后再根据面面垂直的判定定理即可得证.
解答:
解:(1)如图,因为C1D1∥B1A1,所以∠MA1B1为异面直线A1M和C1D1所成的角,
∵A1B1⊥面BCC1B1
∴∠A1B1M=90°
∵A1B1=1,B1M=
∴tan∠MA1B1=
即异面直线A1M和C1D1所成的角的正切值为
.
(Ⅱ)∵A1B1⊥面BCC1B1,BM?面BCC1B1
∴A1B1⊥BM①
由(1)知B1M=
,BM=
,B1B=2
∴BM⊥B1M②
∵A1B1∩B1M=B1
∴由①②可知BM⊥面A1B1M
∵BM?面ABM
∴平面ABM⊥平面A1B1M.
∵A1B1⊥面BCC1B1
∴∠A1B1M=90°
∵A1B1=1,B1M=
| 2 |
∴tan∠MA1B1=
| 2 |
即异面直线A1M和C1D1所成的角的正切值为
| 2 |
(Ⅱ)∵A1B1⊥面BCC1B1,BM?面BCC1B1
∴A1B1⊥BM①
由(1)知B1M=
| 2 |
| 2 |
∴BM⊥B1M②
∵A1B1∩B1M=B1
∴由①②可知BM⊥面A1B1M
∵BM?面ABM
∴平面ABM⊥平面A1B1M.
点评:本题主要考查异面直线所成角的定义以及面面垂直的证明,属常考题型,较难.解题的关键是要掌握异面直线所成角的定义(即将异面直线转化为相交直线所成的角)和面面垂直的判定定理.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
如图,在正方体ABCD-A1B1C1D1中,E为BC1的中点,则DE与面BCC1B1所成角的正切值为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点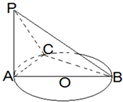 如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )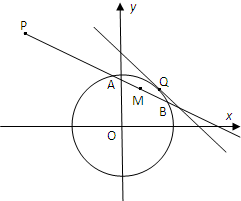 过点P(-4,4)作直线l与圆O:x2+y2=4相交于A、B两点.
过点P(-4,4)作直线l与圆O:x2+y2=4相交于A、B两点.